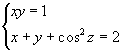358
470
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 1 (8)
Задачи боя Школа 33(3) - Школа 43
25 октября 2000 года
| Страницы: 1 | |
1. | Все стороны выпуклого четырехугольника меньше 20. Доказать, что для любой точки O внутри четырехугольника найдется такая вершина A, что OA < 15. |
17 Марта 2004 17:07 | |
2. | Решите систему уравнений
|
17 Марта 2004 17:08 | |
3. | В четырехугольнике ABCD точка E — середина AB, F — середина CD. Доказать, что середины отрезков AF, BF, CE и DE являются вершинами параллелограмма. |
17 Марта 2004 17:08 | |
4. | Квадратная клетчатая таблица 3 ´ 3 заполнена числами так, что суммы чисел во всех квадратах 2 ´ 2 равны между собой. Доказать, что равны и суммы чисел на диагоналях. |
17 Марта 2004 17:12 | |
5. | На каждой из планет сидит астроном, который наблюдает ближайшую. Доказать, что если число планет нечетно, то одну планету никто не наблюдает. Расстояния между планетами все различны. |
17 Марта 2004 17:13 | |
6. | Даны числа a0, a1, …, a2000, a2001. Известно, что все числа кроме крайних равны сумме соседних с ними чисел. Найти a2001, если известно, что a0 = 1. |
17 Марта 2004 17:14 | |
7. | Решить в целых числах уравнение x4 + 4y4 = 2(z4 + 4u4). |
17 Марта 2004 17:15 | |
8. | На плоскости дано несколько кругов, занимающих площадь 1. Доказать, что можно выбрать несколько непересекающихся кругов, площадь которых не меньше 1/9. |
17 Марта 2004 17:16 | |
| Страницы: 1 | |