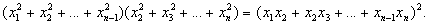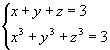1/4 финала. Вариант 1 (8)

1.

Доказать, что из трех отрезков с длинами a > 0, b > 0, c > 0 можно построить треугольник тогда и только тогда, когда pa² + qb² > pqc² для любых чисел p и q, связанных соотношением p + q = 1.

2.

Бесконечная последовательность чисел x₁, x₂, x₃, …, x_n, … (x₁ ¹ 0) при любом n ³ 3 удовлетворяет условию

Доказать, что x₁, x₂, x₃, …, x_n, … являются последовательными членами геометрической прогрессии.

3.

Доказать, что в круге радиуса 1 нельзя выбрать более пяти точек, попарные расстояния между которыми больше 1.

4.

Доказать, что если квадрат натурального числа содержит нечетное число десятков, то цифра единиц квадрата всегда равна 6.

5.

Выпуклый четырехугольник разрезан на пять треугольников. Доказать, что некоторая сторона четырехугольника является стороной одного из треугольников.

6.

В теннисном турнире участвовало n женщин и 2n мужчин. Каждые два участника встретились один раз. Отношение числа побед, одержанных женщинами, к числу побед, одержанных мужчинами, равно 7 : 5. Найти n.

7.

При любом положительном l все корни уравнения ax² + bx + c + l = 0 (a, b, c Î R) вещественны и положительны. Доказать, что a = 0.

8.

Решить в целых числах систему уравнений