358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига и лига 9 классов (8)
| Страницы: 1 | |
1. | Имеется 2002 точки, никакие три из которых не лежат на одной прямой. Каждая пара точек соединена отрезком. Можно ли окрасить каждый отрезок в один из шести заданных цветов так, чтобы не оказалось ни одного треугольника, все стороны которого имеют одинаковые цвета? |
28 Февраля 2004 22:25 | |
2. | Докажите, что для любого натурального n > 1 существует набор из 2n попарно различных натуральных чисел а1, а2, …, аn, b1, b2, …, bn такой, что а1! × а2! × … × аn! = b1! × b2! × … × bn!. (Cимволом m! обозначают произведение всех натуральных чисел от 1 до m включительно: m! = 1 × 2 × … × m). |
28 Февраля 2004 22:26 | |
3. | В восьми банках сидят 80 пауков. Разрешается выбрать любые две банки, в которых суммарное число пауков четное, и пересадить часть пауков из одной банки в другую так, чтобы их стало поровну. Верно ли, что независимо от начального размещения пауков такими операциями можно добиться того, чтобы в банках оказалось поровну пауков? |
28 Февраля 2004 22:26 | |
4. | На плоскости изображены оси координат и график функции y = 1 / (8x). Масштаб по обеим осям одинаков, но не указан на чертеже. Постройте точку с координатами (1; 1), пользуясь только циркулем. |
28 Февраля 2004 22:27 | |
5. | Найдите все простые р, для которых среди дробей |
28 Февраля 2004 22:31 | |
6. | Клетки квадрата 11 ´ 11 раскрашены в белый и черный цвета. У каждой клетки соседей одного с ней цвета меньше, чем соседей противоположного цвета (соседними считаются клетки, имеющие общую сторону). Каково наибольшее возможное количество белых клеток? |
28 Февраля 2004 22:32 | |
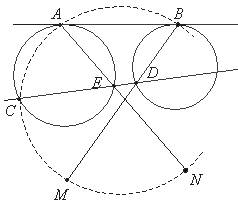
7. | Через точку пересечения внешних касательных к двум окружностям проведена секущая CD и касательная AB, как показано на рисунке. Лучи AE и BD пересекают окружность, проведенную через точки A, B и C, в точках M и N. Докажите, что прямые CD и MN параллельны.
|
28 Февраля 2004 22:32 | |
8. | Окружность разбита пятьюдесятью точками на 50 дуг длиной 1, 2, …, 50. Известно, что длины любых двух противоположных дуг различаются на 25. Докажите, что 50-угольник с вершинами в этих точках имеет хотя бы две параллельные стороны. |
28 Февраля 2004 22:34 | |
| Страницы: 1 | |
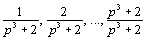 имеется ровно (р + 2) несократимых.
имеется ровно (р + 2) несократимых.