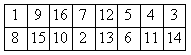Весна 2002 года (24)

1.

Как погрузить 21 бочку, из которых семь полны кваса, семь пусты, а семь заполнены наполовину, на три грузовика, чтобы на всех грузовиках было поровну бочек и кваса?

2.

Что больше: 102102102 × 103103 или 103103103 × 102102?

3.

Какова последняя цифра произведения всех нечётных трёхзначных чисел (от 101 до 999)?

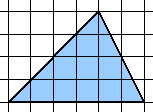
4.

Разрежьте треугольник, изображённый на рисунке, на несколько частей, из которых можно сложить прямоугольник.

5.

Можно ли написать число из одних четвёрок (444...444), которое бы делилось на 8? (Приведите пример или объясните, почему такого числа нет.)

6.

Разделите полоску на четыре равные части, чтобы все части имели одну и ту же сумму входящих в них чисел.

7.

Имеются четыре игровых автомата.
Первый автомат взамен вложенной в него карточки с числом X выдает карточку с числом 2 + X, второй – с числом 2 – X, третий – 2 × X, четвертый – 2 : X (X ¹ 0).
Как с помощью этих автоматов из карточки, на которой написано число 1, получить карточку с числом 19/96?

8.

Алеша, Вася и Саша состязались в беге на 100 метров. Когда Алеша финишировал, Вася отставал от него на 10 м. Когда Вася финишировал, Саша отставал от него на 10 м. На сколько отставал Саша от Алеши, когда Алеша закончил бег?

9.

Сколько было брёвен, если после 57 распилов получилось 103 полена?

10.

На гранях кубика написаны шесть различных цифр. Сумма цифр на противоположных гранях одна и та же для каждой пары параллельных граней. Каковы остальные три цифры, если три известны: 4, 5 и 8? (Перечислите все возможные варианты и докажите, что других нет.)

11.

Найдите наибольший общий делитель всех четырехзначных чисел, записанных при помощи цифр 3, 4, 5, 6.

12.

Можно ли равносторонний треугольник разрезать на:
а) 4; б) 6; в) 7; г) 8
равносторонних треугольников (не обязательно равных друг другу)?

д) Покажите, как разрезать равносторонний треугольник на любое количество равносторонних треугольников (не обязательно равных между собой), начиная с 9.

13.

Как заменить все звездочки на рисунке 10 нечетными цифрами, чтобы получился верный пример на умножение?

Найдите все варианты ответа и докажите, что других нет.

14.

Верно ли, что из любых 100 целых чисел можно выбрать два числа, сумма которых делится на 37?

15.

Бился Иван–Царевич со Змеем Горынычем, трехглавым и треххвостым. Одним ударом он мог срубить либо одну голову, либо один хвост, либо две головы, либо два хвоста. Но, если срубить один хвост, то вырастут два; если срубить два хвоста – вырастет голова; если срубить голову, то вырастает новая голова, а если срубить две головы, то не вырастет ничего. Как должен действовать Иван - Царевич, чтобы срубить Змею все головы и все хвосты?

16.

Два пирата играли на золотые монеты. Сначала первый проиграл половину своих денег (отдал второму), потом второй проиграл половину своих, потом снова первый проиграл половину своих. В результате у первого оказалось 15 монет, а у второго – 33. Сколько монет было у первого пирата до игры?

17.

Число 11…1 записано при помощи n единиц. При каких n это число делится на 41?

18.

Алик, Боря и Вася собирали грибы. Боря собрал грибов на 20% больше, чем Алик, но на 20% меньше, чем Вася. На сколько процентов больше, чем Алик, собрал грибов Вася?

19.

Можно ли расставить числа от 1 до 17 по кругу так, чтобы любые два соседних числа давали в сумме простое число? (Если можно – приведите пример, если нет – объясните, почему.)

20.

Можно ли прямоугольник размером 35 ´ 23 разрезать на прямоугольники размером 5 ´ 7?
(Если можно – приведите пример, если нет – объясните, почему.)

21.

Каких пятизначных чисел больше: не делящихся на 5 или тех, у которых ни первая, ни вторая слева цифры не пятерки?

22.

Девять друзей живут в разных квартирах одного 55-квартирного дома. Когда я пытался выяснить у них, кто где живет, то в ответ услышал следующие заявления:
Андрей: Номер моей квартиры на 23 больше, чем у Бориса.
Борис: Номер моей квартиры на 16 меньше, чем у Виктора.
Виктор: Номер моей квартиры на 19 меньше, чем у Григория.
Григорий: Номер моей квартиры на 12 больше, чем у Дмитрия.
Дмитрий: Номер моей квартиры на 30 больше, чем у Евгения.
Евгений: Номер моей квартиры на 17 меньше, чем у Ивана.
Иван: Номер моей квартиры на 37 меньше, чем у Константина.
Константин: Номер моей квартиры на 12 больше, чем у Леонида.
Леонид: Номер моей квартиры на 10 больше, чем у Андрея.

Впоследствии было установлено, что сведения, которые дал один из друзей ошибочны. Определите, кто где живет?

23.

Математик, получив гонорар за книгу, сказал: “Какое необычное четырехзначное число! Если его разделить на 10, то остаток будет 9, если его разделить на 9, то остаток будет 8, и так далее. В конце концов, когда мы разделим это число на 2, остаток будет равен 1”. Каков же был размер его гонорара, если известно, что он не превышал трех тысяч?

24.

Известно, что календари на некоторые годы одинаковы (в них совпадают и числа и дни недели). Сколько различных календарей нужно иметь в архиве, чтобы не покупать новых в течение всего XXI века?