358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Командная олимпиада (10)
| Страницы: 1 | |
1. | Вычислите: 1 + 2 – 3 – 4 + 5 + 6 – 7 – 8 + ... + 301 + 302. |
16 Ноября 2003 12:10 | |
2. | Грани игральных кубиков занумерованы числами 1, 2, ..., 6 правильно — сумма чисел, записанных на противоположных гранях, равна 7. Строится высотное здание: ставится один кубик на другой так, что сумма соприкасающихся граней равна 8. Какое максимальное число этажей будет в здании? |
16 Ноября 2003 12:10 | |
3. |
Можно ли в клетки таблицы 4 ´ 4 записать числа 1, 2, 3, ..., 16 так, чтобы сумма чисел в каждой строчке делилась на 3? |
16 Ноября 2003 12:11 | |
4. | Сколько существует шестизначных чисел, в записи которых встречается сочетание цифр 1997 (в том же порядке друг за другом)? |
16 Ноября 2003 12:11 | |
5. | Два школьника пришли покупать буквари. Одному не хватило семи копеек, другому — копейки. Они сложили свои деньги, но все равно их не хватило. Сколько стоит букварь? |
16 Ноября 2003 12:12 | |
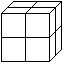
6. |
Каждая грань кубика разбита на четыре равных квадрата (смотри рисунок). В каждый такой квадратик вписали либо число 19, либо число 97. Обязательно ли найдется две грани кубика, суммы чисел на каждой из которых равны? |
16 Ноября 2003 12:13 | |
7. | Можно ли натуральные числа от 1 до 100 выписать в ряд так, чтобы разность любых двух соседних (из большего вычитают меньшее) была не меньше 50? |
16 Ноября 2003 12:13 | |
8. | Каждое из двух различных натуральных чисел умножили на каждую его ненулевую цифру. Могли ли получиться равные результаты? |
16 Ноября 2003 12:14 | |
9. | Какое наименьшее положительное значение может принять разность двух правильных обыкновенных дробей, если знаменатель одной — 8, а другой — 13? |
16 Ноября 2003 12:14 | |
10. | Можно ли по кругу записать 8 чисел, не все из которых равны нулю, чтобы каждое из них было равно сумме трех следующих за ним по часовой стрелке? |
16 Ноября 2003 12:15 | |
| Страницы: 1 | |