358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 3 (8)
| Страницы: 1 | |
1. | В Чебабурге имеют хождение монеты трех видов: 1, 2 и 5 талеров. Масса каждой монеты одного из видов (в унциях) совпадает с ее достоинством (в талерах), масса каждой монеты другого вида в полтора раза больше ее достоинства, а масса каждой монеты третьего вида — в два раза больше. Имеется неограниченный запас монет каждого вида и чашечные весы без гирь. Какое наименьшее количество взвешиваний позволит наверняка определить массу монет каждого достоинства? |
10 Ноября 2003 22:14 | |
2. | В равнобедренном треугольнике ABC (AB = BC) проведена биссектриса AM. Найдите углы треугольника, если известно, что BM = AC. |
10 Ноября 2003 22:15 | |
3. | Пусть M — конечное подмножество множества целых чисел, причем количество элементов в M кратно четырем, а между любыми двумя числами, не принадлежащими M, расположено четное количество элементов из M. Докажите, что M можно разбить на две части с равным числом элементов и равной суммой. |
10 Ноября 2003 22:17 | |
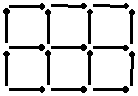
4. |
Клетчатый прямоугольник 2 ´ 3 сложен из 17 спичек, как показано на рисунке. Какие размеры может иметь клетчатый прямоугольник, составленный из 1000 таких же спичек? |
10 Ноября 2003 22:21 | |
5. | На стороне АВ равностороннего треугольника АВС, отмечена точка C1 , а на стороне АС — точка В1 так, что ВC1 = AВ1 = АВ : 3; М — точка пересечения отрезков ВВ1 и СC1. Найдите угол АМС. |
10 Ноября 2003 22:22 | |
6. | Можно ли в кубе с ребром 2000 разместить 7 точек так, чтобы расстояние между любыми двумя было бы больше 2001? Точки можно помещать и на поверхности куба. |
10 Ноября 2003 22:24 | |
7. | Целые числа x, y, z таковы, что числа xy + 1, yz + 1 и zx + 1 являются полными квадратами. Докажите, что произведение xyz делится на 8. |
10 Ноября 2003 22:24 | |
8. | Решите систему уравнений:
|
15 Января 2004 22:53 | |
| Страницы: 1 | |
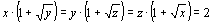 .
.