358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2001 года (25)
| Страницы: 1 | |
1. | Разрежьте кораблик на две части так, чтобы из них можно было сложить квадрат.
|
6 Марта 2004 17:38 | |
2. | На трех банках с вареньем рассеянная хозяйка сделала надписи: “Малина”, “Клубника”, “Земляника или малина”. Определите сорта варенья в каждой банке, если известно, что все надписи не верны. |
6 Марта 2004 17:39 | |
3. | Можно ли в ряду чисел 1 2 3 4 5 6 7 8 9 10 11 12 так расставить во всех промежутках между числами знаки “+” и “–”, чтобы в результате получился 0? |
6 Марта 2004 17:39 | |
4. | 3 кренделя, 5 коврижек и 6 баранок стоят вместе 24 пенса. Что дороже: крендель или баранка? |
6 Марта 2004 17:40 | |
5. | Определите (без транспортира) угол, который стрелки часов составляют в 9 часов 20 минут. Ответ поясните. |
6 Марта 2004 17:40 | |
6. | Прыгая по лестнице с пятого этажа, Алиса насчитала 100 ступенек. Сколько ступенек она насчитала бы, прыгая со 2 этажа? |
6 Марта 2004 17:40 | |
7. | В корзине лежат 20 грибов: белые, подосиновики и подберезовики. Сколько в ней белых грибов, если подберезовиков в ней в 9 раз больше, чем подосиновиков? |
6 Марта 2004 17:41 | |
8. | Кролик на бегу уронил часы и они разбились. Мог ли циферблат расколоться на:
|
6 Марта 2004 17:41 | |
9. | Валет (В) разделил 7 кренделей на три части с Б и С. На допросе в суде 5 свидетелей показали:
Сколько кренделей получил каждый, если все свидетели сказали поровну? |
6 Марта 2004 17:42 | |
10. |
|
6 Марта 2004 17:43 | |
11. | На столе лежат три красные палочки разной длины, причем сумма их длин равняется 30 см и пять синих палочек, сумма длин которых тоже равняется 30 см. Можно ли распилить те и другие палочки так, чтобы их потом можно было расположить парами, и в каждой паре длины палочек были одинаковы, а цвета разные? |
6 Марта 2004 17:44 | |
12. | Пять олимпийских колец разбивают плоскость на 15 частей (не считая бесконечной части). Разместите в этих частях по одному числу из набора от 1 до 15 так, чтобы сумма чисел внутри каждого круга равнялась 39. |
6 Марта 2004 17:45 | |
13. | Каждая грань кубика разбита на 4 равных квадрата. В каждый такой квадратик вписали либо число 19, либо число 97. Обязательно ли найдутся две грани кубика, суммы чисел на каждой из которых равны? |
6 Марта 2004 17:45 | |
14. | Полдник бывает в полдень, а в полдень стрелки часов совпадают. Когда они совпадут в следующий раз? |
6 Марта 2004 17:46 | |
15. | Парусник, пароход и теплоход назывались “Вашингтон”, “Линкольн” и “Джефферсон”, но не обязательно в таком порядке. Порты их отправления и прибытия в алфавитном порядке: Бермуды, Бостон, Галифакс, Лондон, Ньюпорт и Нью-Йорк. Известно, что:
Как называется каждый из кораблей, откуда он отправился и куда плыл? |
6 Марта 2004 17:46 | |
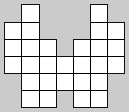
16. | Разрезать фигуру, изображенную на рисунке, на 4 равные по площади и по форме части.
|
6 Марта 2004 17:47 | |
17. | Найдите четыре обыкновенные правильные несократимые дроби, знаменатели которых различны, а сумма дробей равна 3. |
6 Марта 2004 17:47 | |
18. | Найдите все решения ребуса ПЧЁЛКА × 7 = ЖЖЖЖЖЖ (каждая буква соответствует цифре: одинаковые буквы – одинаковым цифрам, разные – разным). |
6 Марта 2004 17:48 | |
19. | Сколько существует трехзначных чисел, у которых одна из цифр равна сумме двух других. |
6 Марта 2004 17:57 | |
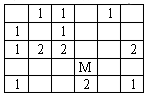
20. | В игре “Сапер” в каждой клетке таблицы стоит либо мина, либо число, которое показывает, сколько мин находится в соседних (по стороне и вершине) с ней клетках. В таблице показано содержимое некоторых клеток (М – мина). Сколько всего мин на поле?
|
6 Марта 2004 17:48 | |
21. | Одно четырехзначное число составлено из последовательных цифр, расположенных в порядке возрастания, второе число составлено из тех же цифр, но в порядке убывания, третье четырехзначное число также составлено из этих четырех цифр. Что это за числа, если их сумма равна 12300? |
6 Марта 2004 17:50 | |
22. | Может ли шахматный конь попасть из левого нижнего угла шахматной доски в правый верхний, побывав на каждом из полей ровно по одному разу? (Если да, то приведите пример его ходов, если нет – обоснуйте.) |
6 Марта 2004 17:51 | |
23. | Сколькими нулями оканчивается произведение всех целых чисел от 1 до 150? |
6 Марта 2004 17:52 | |
24. | Квадрат 5 ´ 5 хотят разрезать на прямоугольники двух видов: 1´4 и 1´3. Может ли после разрезания получиться:
|
6 Марта 2004 17:53 | |
25. | Имеется набор из 6 карточек, на которых написаны числа 1, 2, 3, 4, 5, 6. Можно выбрать ровно k способами набор карточек с суммой S (без учета порядка). Верно ли, что:
|
6 Марта 2004 17:54 | |
| Страницы: 1 | |
 Из шахматной доски 8 ´ 8 вырезали две угловые противоположные клетки (а1 и h8). Можно ли оставшуюся часть разрезать на доминошки (прямоугольники 1 ´ 2 клетки)?
Из шахматной доски 8 ´ 8 вырезали две угловые противоположные клетки (а1 и h8). Можно ли оставшуюся часть разрезать на доминошки (прямоугольники 1 ´ 2 клетки)?