358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2001 года (25)
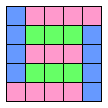
Квадрат 5 ´ 5 хотят разрезать на прямоугольники двух видов: 1´4 и 1´3. Может ли после разрезания получиться:
|
a) Ответ: может (см. рисунок).
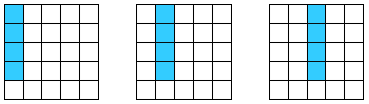
б) Ответ: не может. Наименьшая площадь, которую будут занимать 9 прямоугольников, равна 9 × 3 = 27, а это больше, чем площадь самого квадрата, равная 25. Поэтому 9 прямоугольников получиться не может. в) Ответ: не может. Если прямоугольник 1 × 4 один, то прямоугольников 1 × 3 семь и их общая площадь равна 25. Если увеличивать количество прямоугольников 1 × 4, то площадь, занимаемая ими, будет увеличиваться на 4. Но тогда количество прямоугольников 1 × 3 будет уменьшаться, и площадь, занимаемая ими, будет уменьшаться на 3. При этом общая площадь всех прямоугольников будет увеличиваться на 1, то есть будет больше 25. Значит, подходит только первый вариант, когда прямоугольник 1 × 4 один. Рассмотрим, где он может располагаться. Основных положений три (см. рисунок) — все остальные положения можно получить из этих, поворачивая квадрат.
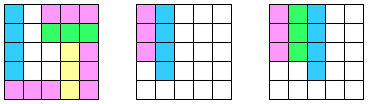
Во всех трех случаях однозначно вырезается несколько прямоугольников 1 × 3, после чего нельзя в оставшееся место поставить прямоугольники 1 × 3 (см. рисунок).
|
6 Марта 2004 17:53 Раздел каталога :: Ссылка на задачу
|