Задачи второго тура боев (15)

1.

Вася сосчитал знакопеременную сумму ряда 2, 4, 8, …, 2⁹⁸:

2 + 4 – 8 + … + 2⁹⁸,

а Петя — обычную:

2 + 4 + 8 + … + 2⁹⁸.

Во сколько раз результат Васи меньше результата Пети?

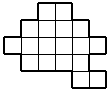
2.

Разрежьте фигуру, изображенную на рисунке, на 3 равные части.

3.

Можно ли в каждом из равенств
БУ + РА + ТИ = НО,
ПИ + НО + КК = ИО
заменить одинаковые буквы одинаковыми цифрами, а разные — разными так, чтобы оба этих равенства оказались верными?

4.

Можно ли на доску 5 ´ 5 поставить 3 коня так, чтобы они били все незанятые ими клетки?

5.

Однажды Саша посмотрел на свои электронные часы и заметил удивительную вещь: если сравнить их показание сейчас и в тот момент, когда Саша последний раз смотрел на часы, то цифры стоят в том же порядке, но одна цифра исчезла. Мало того, если бы у Саши были часы со стрелками, то сравнения ничего бы не дало: часы показывали то же время. Который сейчас час?

6.

Сколько трехзначных чисел, у которых одна из цифр равна сумме двух других?

7.

У каждого из 10 ребят были наклейки с изображением Майкла Джексона. Первый сказал, что, по крайней мере, у него одна наклейка имеется. “А у меня ровно на одну больше!” — сказал второй. “А у меня ровно на одну больше, чем у тебя!” — сказал третий второму, затем такую же фразу произнес четвертый — третьему, …, девятый — восьмому. А десятый девятому заявил: “У меня наклеек больше, чем у тебя!”. Сколько наклеек у каждого, если все ребята оказались правы, а всего у них 64 наклейки?

8.

К каждой грани кубика приклеили по такому же кубику. К каждой грани поверхности получившейся фигуры приклеили еще раз по такому же кубику (возможно, некоторые кубики закрыли две грани). Из какого количества квадратиков состоит поверхность полученного тела?

9.

Решите уравнение: 1 – (2 – (3 – (…(1997 – (1998 – x))…))) = 999.

10.

Между какими цифрами (можно спереди или в конце) в числе 199999 надо вставить цифру, и какую, чтобы получившееся число делилось на 1998?

11.

Сколько существует 10-значных чисел, в записи которых использованы только цифры 1, 2, 3 и любые две соседние цифры отличаются на 1?

12.

В одной клетке бесконечной шахматной доски стоит фигура, которая за один ход может переместиться либо на 3 клетки по вертикали и 4 клетки по горизонтали, либо на 4 клетки по вертикали и 3 клетки по горизонтали. Докажите, что такая фигура из любой клетки доски может попасть за несколько ходов в любую другую клетку.

13.

Протокол заседания владельцев участков товарищества “Урожай” гласит, что
1) при выборе нового председателя против кандидата проголосовало ровно 34% присутствующих (сам кандидат в голосовании не участвовал);
2) против сметы расходов на следующий год проголосовало ровно 44% всех присутствующих.
Могло ли такое произойти?

14.

Можно ли из единичных кубиков склеить тело, поверхность которого состоит из нечетного числа единичных квадратиков? (Любые два кубика либо склеены по грани, либо их грани не соприкасаются.)

15.

Можно ли квадрат со стороной 20см разрезать на 10 попарно неравных квадратов, длины сторон которых выражаются целым числом сантиметров?