358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Задачи второго тура боев (15)
В одной клетке бесконечной шахматной доски стоит фигура, которая за один ход может переместиться либо на 3 клетки по вертикали и 4 клетки по горизонтали, либо на 4 клетки по вертикали и 3 клетки по горизонтали. Докажите, что такая фигура из любой клетки доски может попасть за несколько ходов в любую другую клетку. |
|
25 Ноября 2003 19:56 Раздел каталога :: Ссылка на задачу
|
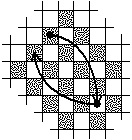 Раскрасим доску в шахматном порядке. Заметим, что фигура с белой клетки всегда ходит на черную, а с черной
— на белую. На рисунке видно, что фигура может попасть на любую соседнюю клетку того же цвета.
Значит, фигура с черной клетки может попасть на любую черную клетку. Также она может попасть на белую клетку,
и таким же образом обходить белые клетки. Значит, фигура с любой клетки может добраться до любой другой.
Раскрасим доску в шахматном порядке. Заметим, что фигура с белой клетки всегда ходит на черную, а с черной
— на белую. На рисунке видно, что фигура может попасть на любую соседнюю клетку того же цвета.
Значит, фигура с черной клетки может попасть на любую черную клетку. Также она может попасть на белую клетку,
и таким же образом обходить белые клетки. Значит, фигура с любой клетки может добраться до любой другой.