Задачи первого тура боев (11)

1.

На 22 карточках написаны натуральные числа 1, 2, …, 22. Из этих карточек составили 11 дробей. Какое наибольшее число этих дробей могут иметь целые значения?

2.

Из трех квадратов, длины сторон которых составляют целое число сантиметров, сложили прямоугольник.
a) Найти его периметр, если площадь равна 96см²?
b) Найти его площадь, если периметр равен 50см?

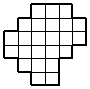
3.

Разрежьте фигуру, изображенную на рисунке, на 4 равные части:

4.

Два мудреца написали на семи карточках числа от 5 до 11. После этого они перемешали карточки, первый мудрец взял себе три карточки, второй взял две, а оставшиеся они, не глядя, убрали в мешок. Изучив свои карточки, первый мудрец сказал второму: "Я знаю, что сумма чисел на твоих карточках четна!" Какие числа написаны на карточках первого мудреца? Единственный ли ответ в этой задаче?

5.

a) Можно ли в таблице 5 ´ 5 расставить 5 единиц, 5 двоек, 5 троек, 5 четверок и 5 пятерок так, чтобы сумма чисел в любом квадрате 2 ´ 2 была одной и та же?

b) Можно ли в таблице 7 ´ 7 расставить 7 единиц, 7 двоек, …, 7 семерок так, чтобы сумма чисел в любом квадрате 3 ´ 3 была одной и та же?

c) Можно ли в таблице 6 ´ 6 расставить 6 единиц, 6 двоек, …, 6 шестерок так, чтобы сумма чисел в любом квадрате 3 ´ 3 была одной и та же?

6.

Каких пятизначных чисел больше: тех, у которых наименьшая цифра стоит третьей, или тех, у которых наименьшая цифра первая?

7.

Можно ли расставить по кругу
a) 5 чисел так, чтобы любые два из них, не стоящие рядом, отличались друг от друга на 6?
b) 99 чисел так, чтобы любые два числа, между которыми стоит ровно 48 чисел, отличаются на 1?
c) 99 чисел так, чтобы любые два числа, между которыми стоит ровно 4 числа, отличаются на 1?

8.

Имеет ли решение ребус: СВЕТА – ДИМА = САША? (Одинаковые цифры заменены одинаковыми буквами, разные — разными.)

9.

Можно ли фигуру, изображенную на рисунке, разрезать на 4 равные части двумя различными способами?

10.

Можно ли на плоскости отметить 6 точек и несколько прямых так, чтобы через каждые две отмеченные точки проходила отмеченная прямая, и через каждую точку проходило ровно три отмеченные прямые?