Вариант боев 2 (8)

1.

Среди первых 60 натуральных чисел произвольно выбрано 30 + n (где 1 £ n £ 30) различных чисел.
Докажите, что среди выбранных чисел всегда найдутся 2n чисел таких, что их сумма равна 61n.

2.

Решите в натуральных числах x, y, z и t уравнение x² + y² + z² = 2^t.

3.

Играя в домино, Мустафа, Табриз, Гамид и Эльмир взяли по семь костей с различной суммой очков. При этом сумма очков Мустафы и Табриза оказалась равной сумме очков Гамида и Эльмира, а разница очков Мустафы и Табриза составила 27 / 7 разницы очков Гамида и Эльмира. Укажите какие-нибудь 12 костей домино, которые находятся на руках у Мустафы и Табриза.

4.

Из бумаги склеили правильный тетраэдр. Разрежьте его на 12 одинаковых бумажных равносторонних треугольников.

5.

Могут ли длины сторон x, y и z какого-нибудь треугольника удовлетворять неравенству:

x³ + y³ + z³ + 2xyz ³  x²(y + z) + y²(z + x) + z²(x + y)?

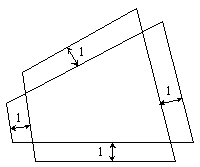
6.

У крестообразно пересекающихся четырехугольников соответствующие стороны параллельны и отстоят друг от друга на расстояние 1, как показано на рисунке. Докажите, что периметры четырехугольников равны.

7.

В некоторых клетках шахматной доски проведена одна из двух возможных диагоналей так, что ни для каких двух диагоналей концы их не совпадают. Какое наибольшее количество диагоналей можно провести, соблюдая такое условие?

8.

Дан выпуклый шестиугольник ABCDEF, в котором AB = CD = EF, ÐA = ÐC = ÐE и ÐB = ÐD = ÐF. Докажите, что BC = DE = FA.