358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 2 (8)
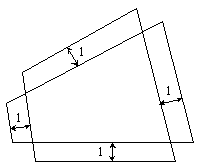
У крестообразно пересекающихся четырехугольников соответствующие стороны параллельны и отстоят друг от друга на расстояние 1, как показано на рисунке. Докажите, что периметры четырехугольников равны. |
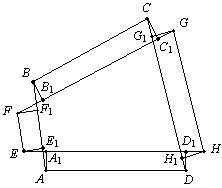
Решение. Пусть ABCD и EFGH — данные четырехугольники, АA1, ВВ1, СС1, DD1, EE1, FF1, GG1, HH1 — перпендикуляры к EH, FG, FG, EH, AB, AB, CD, CD соответственно (показано на рисунке). Прямоугольные треугольники AEE1 и AEA1 равны по гипотенузе и катету (АА1 = ЕЕ1 = 1), поэтому АЕ1 = А1Е. Аналогично F1B = FB1, CG1 = C1G, H1D = HD1. Имеем равенства АВ = АЕ1 + EF1 + FB1 = AE1 + EF + F1B, BC = FG – FB1 – CG1, CD = CG1 + G1H1 + H1D = СG1 + GH + H1D, DA = HE – HD1 – AE1, из которых следует, что AB + BC + CD + DA = = EF + FG + GH + HE + (АЕ1 – А1Е) + (F1B – FB1) + (CG1 – C1G) + (H1D – HD1) = = EF + FG + GH + HE. Что и требовалось доказать. |
Автор задачи — В. Произволов, г. Москва |
10 Ноября 2003 22:11 Раздел каталога :: Ссылка на задачу
|