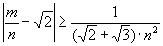1863
358
471

всего задач:
всего разделов:
активных пользователей:

О проекте : Математика : Химия : Регистрация : Ссылки : Помощь

… > Седьмой турнир (2000-2001 уч.г… > 1/4 финала. Вариант 2

30 мартра 2005

Форумы снова функционируют.

21 декабря 2004

Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.

29 сентября 2004

Форум обновился до версии 2.0.10

15 мая 2004

Новый раздел: "Программирование"

16 апреля 2004 года

Задачи Ярославского турнира математических боев — 124 задачи с решениями.

29 марта 2004

Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.

$СУНЦ МГУ - Школа им. А. Н. Колмогорова.\r\nОфициальный сайт$

1/4 финала. Вариант 2 (8)

Гимназия (г.Ростов) - Школа №33(2) (21 февраля 2001 года)

Страницы: 1
1.	Стороны прямоугольного треугольника — целые числа. Доказать, что его площадь делится на 6.
	16 Апреля 2004 21:11 решение
в корзину


2.	На доске написано несколько нулей, единиц и двоек. Над ними производится следующая операция: стираются две неравные цифры и вместо них записывается цифра, отличная от стертых. После нескольких таких операций на доске осталась единственная цифра. Зависит ли она от порядка, в котором проводились стирания?
	16 Апреля 2004 21:15 решение
в корзину


3.	Доказать, что для любого прямоугольного треугольника справедливо неравенство 0,4 < r / h < 0,5, где r — радиус вписанного круга, h — высота, опущенная на гипотенузу.
	16 Апреля 2004 21:15 решение
в корзину


4.	Доказать, что для любых натуральных m и n справедливо неравенство:
	16 Апреля 2004 21:16 решение
в корзину


5.	Два двузначных числа, записанные одно за другим, образуют четырехзначное число, которое делится на их произведение. Найти все такие пары чисел.
	16 Апреля 2004 21:16 решение
в корзину


6.	Доказать, что квадратное уравнение ax² + bx + c = 0 с целыми нечетными коэффициентами не имеет рациональных корней.
	16 Апреля 2004 21:22 решение
в корзину


7.	Доказать, что основания перпендикуляров, опущенных из произвольной точки окружности на стороны вписанного в нее треугольника, лежат на одной прямой.
	16 Апреля 2004 21:22 решение
в корзину


8.	Доказать, что если n — целое число, большее 1, то 3ⁿ + 1 не делится на 2ⁿ.
	16 Апреля 2004 21:22 решение
в корзину

Страницы: 1

Задач на странице: 5 10 25