358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М801 - М820 (20)
| Страницы: « 1 2 3 4 » | |
11. | M811 Пусть ha, hb, hc — высоты, а ma, mb, mc — медианы остроугольного треугольника (проведенные к сторонам а, b, с), r и R радиусы вписанной и описанной окружностей. Докажите, что
|
28 Января 2004 22:33 | |
12. | M812 Докажите, что при любом натуральном n
|
28 Января 2004 22:35 | |
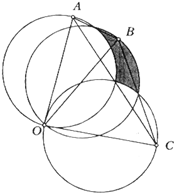
13. | M813
Даны отрезки OА, OB, OС одинаковой длины (точка B лежит внутри угла АОС).
На них как на диаметрах построены окружности.
|
28 Января 2004 22:36 | |
14. | M814 Отметим в натуральном ряду числа, которые можно представить в виде суммы двух квадратов натуральных чисел. Среди отмеченных чисел встречаются тройки последовательных чисел, например 72 = 62 + 62, 73 = 82 + 32, 74 = 72 + 52. а) Объясните, почему не могут встретиться четыре последовательных отмеченных числа. Докажите, что среди отмеченных чисел встретится бесконечно много б) пар, в) троек последовательных чисел. |
28 Января 2004 22:36 | |
15. | M815* На окружности расставлены 4k точек, занумерованных в произвольном порядке числами 1, 2, ..., 4k. а) Докажите, что эти точки можно соединить 2k попарно пересекающимися отрезками так, что разность чисел в концах каждого отрезка не превосходит 3k - 1. б) Постройте пример расстановки номеров, показывающий, что число 3k - 1 в пункте а) нельзя заменить меньшим. |
28 Января 2004 22:37 | |
| Страницы: « 1 2 3 4 » | |
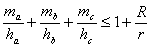 .
.
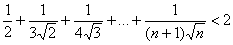 .
.