358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М801 - М820 (20)
| Страницы: 1 2 » | |
1. | M801* Докажите, что для любого натурального n выполнено равенство
([x] обозначает целую часть числа x). |
28 Января 2004 22:22 | |
2. | M802
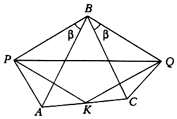
На сторонах AВ и AС треугольника AВС как на гипотенузах построены вне его прямоугольные треугольники AРВ и BQС с одинаковыми углами величины β при их общей вершине B (показано на рисунке). Найдите углы треугольника PQK, где K — середина стороны AС. |
28 Января 2004 22:23 | |
3. | M803 Сумма двух рациональных чисел x и y — натуральное число, сумма обратных к ним чисел 1/х и 1/y — тоже натуральное число. Какими могут быть x и y? |
28 Января 2004 22:24 | |
4. | M804 Точка O — середина оси прямого кругового цилиндра, A и B — диаметрально противоположные точки окружности нижнего основания цилиндра, С — некоторая точка окружности верхнего основания, не лежащая в плоскости OАВ. Докажите, что сумма двугранных углов трехгранного угла OАВС (с вершиной O) равна 2π. |
28 Января 2004 22:24 | |
5. | M805* а) На сторонах BС, СА, AВ треугольника AВС выбраны соответственно точки A1, В1, C1 так, что отрезки AA1, BВ1 и CC1 пересекаются в одной точке. Докажите, что SA1B1C1 £ SABC / 4. б) На гранях BCD, CDA, BDA, ABC тетраэдра ABCD выбраны соответственно точки A1, В1, C1, D1 так, что отрезки AA1, BВ1, CC1, DD1, пересекаются в одной точке. Докажите, что VA1B1C1D1 £ VABCD / 27. |
28 Января 2004 22:27 | |
6. | M806 a) Докажите, что если б) Докажите, что если для некоторого p > 0 |
28 Января 2004 22:28 | |
7. | M807 a) Из произвольной точки M внутри равностороннего треугольника опущены перпендикуляры
MK1, MK2, MK3 на его стороны.
б) Из произвольной точки M опущены перпендикуляры
MK1, MK2, ..., MKn
на все стороны правильного n-угольника (или их продолжения).
в) Из произвольной точки M внутри правильного тетраэдра опущены перпендикуляры
MK1, MK2, MK3, MK4 на его грани.
|
28 Января 2004 22:29 | |
8. | M808 На бесконечном листе клетчатой бумаги двое играют в такую игру: первый окрашивает какую-нибудь клетку
в красный цвет, второй — k (неокрашенных) клеток в синий цвет, затем снова первый одну (неокрашенную)
— в красный, второй — k клеток — в синий и.т.д. Первый стремится к тому, чтобы четыре какие-нибудь
красные клетки расположились в вершинах квадрата (со сторонами, параллельными линиям сетки).
|
28 Января 2004 22:30 | |
9. | M809 Найдите сумму |
28 Января 2004 22:31 | |
10. | M810* Докажите, что в любой выпуклый многоугольник М можно поместить прямоугольник, площадь которого не меньше 1/4 площади многоугольника М. |
28 Января 2004 22:32 | |
| Страницы: 1 2 » | |
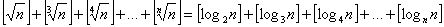
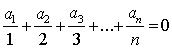 ,
,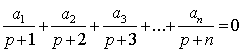 ,
,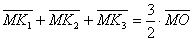 , где O — центр треугольника.
, где O — центр треугольника.
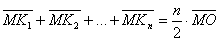 ,
,
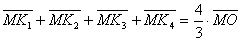 ,
,
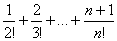 .
.