358
473
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М721 - М740 (20)
| Страницы: 1 2 » | |
1. | M721 Каждая сторона треугольника поделена на три равные части. Точки деления служат вершинами двух треугольников, пересечение которых — шестиугольник. Найдите площадь этого шестиугольника, если площадь данного треугольника равна S. |
18 Января 2004 14:36 | |
2. | M722 В точках A1, A2, ..., An, расположенных по окружности, расставляются в некотором порядке числа 1, 2, ..., n. а) Докажите, что сумма n модулей разностей соседних чисел не меньше 2n - 2. б) Для какого количества расстановок эта сумма равна 2n - 2? |
18 Января 2004 14:37 | |
3. | M723* Существует ли бесконечное множество натуральных чисел такое, что ни одно из чисел этого множества и никакая сумма нескольких из них не является степенью натурального числа (a2, где k ³ 2)? |
18 Января 2004 14:38 | |
4. | M724 По плоскости ползут несколько черепах, скорости которых равны по величине, но различны по направлению. Докажите, что как бы черепахи ни были расположены вначале, через некоторое время они будут находиться в вершинах выпуклого многоугольника. |
18 Января 2004 14:39 | |
5. | M725* Положим qn = Найдите а) q1 и q2, б) q3 и q4. в) Докажите, что qn — рациональное число при любом n. |
18 Января 2004 14:41 | |
6. | M726 Точка внутри правильного 2n-угольника соединена с вершинами. Возникшие 2n треугольников раскрашены попеременно в голубой и красный цвет. Докажите, что сумма площадей голубых треугольников равна сумме площадей красных а) для n = 4, б) для n = 3, в) для любого натурального n. |
18 Января 2004 14:42 | |
7. | M727 Докажите неравенство
|
18 Января 2004 14:43 | |
8. | M728 Пусть А, В, С — вершины параллелепипеда, соседние с его вершиной P, а Q — вершина, противоположная Р. Докажите, что а) расстояния от точек А, В, С до прямой РQ могут служить длинами сторон некоторого треугольника; б) площадь S этого треугольника, объем V параллелепипеда и длина d его диагонали PQ связаны соотношением V = 2dS. |
18 Января 2004 14:45 | |
9. | M729 Найдите натуральное число, обладающее следующим свойством: если записать рядом его квадрат и его куб, а затем переставить написанные цифры в обратном порядке, получится шестая степень этого числа. |
18 Января 2004 14:47 | |
10. | M730* Последовательность (an) определяется условиями
а) Выпишите первые 20 членов последовательности и найдите a1982. б) Докажите, что каждое натуральное число входит в последовательность 2 или 4 раза. Сколько раз встретится в ней число 2k (при каждом k = 1, 2, 3, ...)? в) Докажите, что разность
г) Докажите, что an = n / 3 для бесконечного множества значений n. д) Найдется ли n такое, что разность
е) Докажите, что |
18 Января 2004 14:49 | |
| Страницы: 1 2 » | |
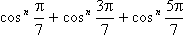 .
.