358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
2. Отношение сторон подобных треугольников (17)
| Страницы: 1 | |||||||||
1. | Задача 1.19 Прямая, проходящая через вершину A квадрата ABCD, пересекает сторону CD в точке E и прямую BC в точке F. Докажите, что
| ||||||||
17 Января 2004 14:51 | |||||||||
2. | Задача 1.20 На высотах BB1 и CC1 треугольника ABC взяты точки B2 и C2 так, что РAB2C = РAC2B = 90°. Докажите, что AB2 = AC2. | ||||||||
17 Января 2004 14:51 | |||||||||
3. | Задача 1.21 В трапецию ABCD (BC || AD) вписана окружность, касающаяся боковых сторон AB и CD в точках K и L соответственно, а оснований AD и BC в точках M и N. а) Пусть Q — точка пересечения отрезков BM и AN. Докажите, что KQ||AD. б) Докажите, что AK · KB = CL · LD. | ||||||||
17 Января 2004 14:52 | |||||||||
4. | Задача 1.22 На стороны BC и CD параллелограмма ABCD (или на их продолжение) опущены перпендикуляры AM и AN. Докажите, что DMAN ~ DABC. | ||||||||
17 Января 2004 14:53 | |||||||||
5. | Задача 1.23 Прямая l пересекает стороны AB и AD параллелограмма ABCD в точках E и F соответственно. Пусть G — точка пересечения прямой l с диагональю AC. Докажите, что
| ||||||||
17 Января 2004 14:55 | |||||||||
6. | Задача 1.24 Пусть AC — большая из диагоналей параллелограмма ABCD. Из точки C на продолжения сторон AB и AD опущены перпендикуляры CE и CF соответственно. Докажите, что AB · AE + AD · AF = AC2. | ||||||||
17 Января 2004 14:55 | |||||||||
7. | Задача 1.25 Углы треугольника ABC связаны соотношением 3a + 2b = 180°. Докажите, что a2 + bc = c2. | ||||||||
17 Января 2004 14:56 | |||||||||
8. | Задача 1.26 Концы отрезков AB и CD перемещаются по сторонам данного угла, причем прямые AB и CD перемещаются параллельно; M — точка пересечения отрезков AB и CD. Докажите, что величина
остается постоянной. | ||||||||
17 Января 2004 14:56 | |||||||||
9. | Задача 1.27 Через произвольною точку P стороны AC треугольника ABC параллельно его медианам AK и CL проведены прямые, пересекающие стороны BC и AB в точках E и F соответственно. Докажите, что медианы AK и CL делят отрезок EF на три равные части. | ||||||||
17 Января 2004 14:56 | |||||||||
10. | Задача 1.28 На биссектрисе угла с вершиной C взята точка P. Прямая, проходящая через точку P, высекает на сторонах угла отрезки длиной a и b. Докажите, что величина
не зависит от выбора этой прямой. | ||||||||
17 Января 2004 14:57 | |||||||||
11. | Задача 1.29 На стороне BC равностороннего треугольника ABC как на диаметре внешним образом построена полуокружность, на которой взяты точки K и L, делящие полуокружность на три равные дуги. Докажите, что прямые AK и AL делят отрезок BC на равные части. | ||||||||
17 Января 2004 14:58 | |||||||||
12. | Задача 1.30 Точка O — центр вписанной окружности треугольника ABC. На сторонах AC и BC выбраны точки M и K соответственно так, что BK · AB = BO2 и AM · AB = AO2. Докажите, что точки M, O и K лежат на одной прямой. | ||||||||
17 Января 2004 14:59 | |||||||||
13. | Задача 1.31
| ||||||||
20 Января 2004 13:46 | |||||||||
14. | Задача 1.33 Отрезок BE разбивает треугольник ABC на два подобных треугольника, причем коэффициент подобия равен | ||||||||
17 Января 2004 15:01 | |||||||||
15. | Задача 1.17 а)В треугольнике ABC проведена биссектриса BD внутреннего или внешнего угла. Докажите, что б) Докажите, что центр O вписанной окружности треугольника ABC делит биссектрису AA1 в отношении | ||||||||
18 Января 2004 15:23 | |||||||||
16. | Задача 1.18 Длины двух сторон треугольника равны a, а длина третьей стороны равна b. Вычислите радиус его описанной окружности. | ||||||||
18 Января 2004 15:51 | |||||||||
17. | Задача 1.32
| ||||||||
18 Января 2004 15:53 | |||||||||
| Страницы: 1 | |||||||||
 Докажите, что если a1 = a2 и b1 = b2, то x = y.
Докажите, что если a1 = a2 и b1 = b2, то x = y.
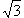 . Найдите углы треугольника ABC.
. Найдите углы треугольника ABC.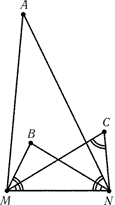 На отрезке MN построены подобные, одинаково ориентированные треугольники AMN, NBM и MNC. Докажите, что треугольник ABC подобен всем
На отрезке MN построены подобные, одинаково ориентированные треугольники AMN, NBM и MNC. Докажите, что треугольник ABC подобен всем