Личная олимпиада (7)

1.

Нарисуйте шестиугольник, который жюри не сможет разрезать на два четырехугольника.

2.

В следующих многозначных числах цифры заменены буквами (одинаковые цифры — одинаковыми буквами, а разные — разными). Оказалось, что ДЕВЯНОСТО делится на 90, а ДЕВЯТКА делится на 9. Может ли СОТКА делиться на 9?

3.

В каждой клетке доски размером 16´30 сидит по жуку. Могут ли жуки перелететь на доску размером 15´32, в каждую клетку по одному жуку, чтобы жуки, бывшие соседями на доске 16´30, оказались соседями и на новой доске? (Соседи — жуки, сидящие в клетках с общей стороной.)

4.

Можно ли первые 2001 натуральных чисел расставить по кругу так, чтобы каждое число делилось на разность своих соседей?

5.

Натуральное число разрешено увеличить на любое целое число процентов от 1 до 100, если при этом получаем натуральное число. Найдите наименьшее натуральное число, которое нельзя при помощи таких операций получить из числа 1.

6.

Двое играют в шахматы, а еще шестеро желающих сыграть образуют очередь. Проигравший партию становится в конец очереди; тот, чья очередь подошла, играет с победителем и так далее. Может ли в какой-то момент оказаться так, что каждые двое cыграли между собой ровно один раз?

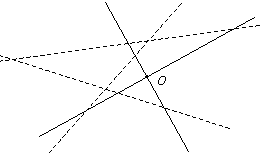
7.

Оси Ox и Oy и прямые y = ax + b, y = bx + c, y = cx + a расположены так, как показано на рисунке. Укажите ось Ox и положительное направление на ней.