358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 6 (8)
Задачи боя "Школа №42 - Школа №49"
25 ноября 2000 года
| Страницы: 1 | |
1. | Какой цифрой оканчивается десятичная запись числа |
17 Марта 2004 20:59 | |
2. | В квадратной таблице N ´ N расставляются числа 0, 1 и 2. При каких N возможно, что среди сумм этой таблицы по строкам и столбцам встретятся все числа от 1 до 2N? |
17 Марта 2004 21:06 | |
3. | Имеется шар, линейка, лист бумаги и циркуль, которым можно рисовать как на плоскости, так и на шаре. Постройте радиус этого шара. |
17 Марта 2004 21:10 | |
4. | Решите уравнение:
|
17 Марта 2004 21:10 | |
5. | Числа a1, a2, …, a2000 таковы, что их сумма и сумма всех их попарных произведений равны нулю. Докажите, что все эти числа равны нулю. |
17 Марта 2004 21:11 | |
6. | Функция f (x) такова, что
Найдите f (1999). |
17 Марта 2004 21:12 | |
7. | Дан параллелограмм OACB. Проведена прямая, отсекающая четверть стороны OA и треть стороны OB, считая от вершины O. Какую часть эта прямая отсекает от диагонали OC? |
17 Марта 2004 21:12 | |
8. | В некоторой стране между любыми двумя городами имеется непосредственное железнодорожное сообщение, но только в одном направлении. Докажите, что существует такой город, из которого можно попасть в любой другой, проезжая не более чем через один промежуточный. |
17 Марта 2004 21:13 | |
| Страницы: 1 | |
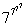 ?
?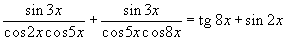
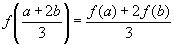 , f (1) = 1, f (4) = 7.
, f (1) = 1, f (4) = 7.