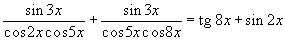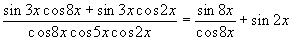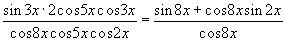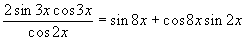358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 6 (8)
Задачи боя "Школа №42 - Школа №49"
25 ноября 2000 года
Решите уравнение:
|
Ответ: x = pk, k Î Z. Выполним некоторые преобразования:
Из исходного уравнения следует, что cos 8x ¹ 0, cos 2x ¹ 0 (так как иначе sin 2x = 0). Далее: sin 2x = 0 Û x = pn / 2, n Î Z. В ходе преобразований могли приобрести лишние корни. Подстановкой можно убедиться, что нечетные значения n нужно исключить из рассмотрения, а при четных n получаем решения уравнения. Таким образом, получаем ответ: x = pk, k Î Z. |
17 Марта 2004 21:10 Раздел каталога :: Ссылка на задачу
|