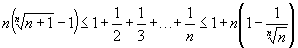358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 3 (8)
Задачи боя Школа №86 - Гимназия №1
3 ноября 2000 года
| Страницы: 1 | |
1. | Докажите неравенство для любого натурального n:
|
17 Марта 2004 17:30 | |
2. | Найти геометрическое место точек, для которых сумма расстояний до двух данных прямых m и l равна длине a данного отрезка. |
17 Марта 2004 17:31 | |
3. | На доске написана разность ********* – ********* = …. Первый игрок называет цифру. Второй ее ставит вместо звездочки. После расстановки всех цифр считается разность. Первый стремится ее увеличить, а второй уменьшить. Какое число получится, если оба игрока будут играть по наилучшей стратегии? |
17 Марта 2004 17:36 | |
4. | На плоскости n параллельных прямых пересекаются серией из m параллельных прямых. Сколько параллелограммов можно выделить в образовавшейся сетке? |
17 Марта 2004 17:37 | |
5. | Доказать, что если натуральное число p = 100a + 10b + c делится на 37, то и числа q = 100b + 10c + a и r = 100c + 10a + b также делятся на 37 (числа a, b, c — натуральные). |
17 Марта 2004 17:38 | |
6. | В данный треугольник ABC вписать с помощью циркуля и линейки прямоугольник (две вершины на AC, остальные на BC и AB), имеющий заданную диагональ. |
17 Марта 2004 17:39 | |
7. | На стороне AB треугольника ABC внешним образом построили квадрат с центром O. Точки M и N — середины сторон BC и AC соответственно; BC = a, AC = b. Найти наибольшее значение OM + ON, если угол ACB меняется. |
17 Марта 2004 17:39 | |
8. | Известно, что последовательность чисел a1, a2, a3, … при любом значении n удовлетворяет соотношению: an+1 – 2an + an–1 = 1, a1 = 1, a2 = 5. Найдите a2000. |
17 Марта 2004 17:41 | |
| Страницы: 1 | |