358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 3 (8)
Задачи боя Школа №86 - Гимназия №1
3 ноября 2000 года
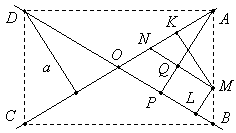
Найти геометрическое место точек, для которых сумма расстояний до двух данных прямых m и l равна длине a данного отрезка. |
Если прямые пересекаются, то искомое геометрическое место точек состоит из четырех отрезков, образующих прямоугольник ABCD, вершины которого лежат на данных прямых m и l и находятся от них на данном расстоянии a. Докажем это. Пусть точка M такова, что MK ^ l, ML ^ m, MK + ML = a, где a — длина данного отрезка. Проведем через M прямую AB так, что OB параллельно MN и OA = OB. Пусть AP ^ OB и Q — точка пересечения AP и MN.
Из равенства AN = MN следует, что MK = AQ, откуда AP = AQ + QP = MK + ML = a. Следовательно, точка A является вершиной упомянутого прямоугольника; то же верно и для точки B, так что M лежит на стороне этого прямоугольника. Обратно: если точка M лежит на стороне этого прямоугольника, то, проведя рассуждение в обратном порядке, получим, что MK + ML = AP = a. Если прямые l и m параллельны и расстояние между ними равно h, то искомое геометрическое место точек существует только тогда, когда a ³ h, и представляет собой пару прямых, параллельных данным, при a > h или всю полосу между l и m при a = h. |
17 Марта 2004 17:31 Раздел каталога :: Ссылка на задачу
|