358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2002 года (25)
| Страницы: « 1 2 3 » | |
11. | Петя и Вася выписывают 12-значное число, ставя цифры по очереди, начиная со старшего разряда. Начинает Вася. Как Пете добиться того, чтобы итоговое число делилось на 9 независимо от ходов Васи? |
9 Марта 2004 20:11 | |
12. | В первенстве по футболу участвует 8 команд. Каждая команда играет с каждой один матч. Команда Меркурий набрала 19 очков, а команда Уран 18. Каков результат матча Меркурий-Уран (ничья, победил Уран, победил Меркурий)? Известно, что за победу присуждается 3 очка, за ничью 1 очко, а за поражение 0 очков. |
9 Марта 2004 20:12 | |
13. | Петя забыл последние 3 цифры телефонного номера, но помнит, что все цифры различны и среди них одна девятка. Какое максимальное число номеров ему придется набрать, чтобы попасть по нужному номеру? |
9 Марта 2004 20:12 | |
14. | В клетках квадратной таблицы 3 × 3 расставлены числа 1, 2, 3, …, 9 так, что сумма каждых четырех чисел, заполняющих квадрат 2 × 2, равна одному и тому же числу S. Найдите все возможные значения S. |
9 Марта 2004 20:13 | |
15. | Масса ста гирек, сваленных в одну кучу, составляет 500 г. Известно, что имеются только гирьки в 1г, 10г, 50г. Сколько в кучке гирек каждой массы? Ответ пояснить. |
9 Марта 2004 20:14 | |
16. | Можно ли в ряду чисел 1 2 3 4 5 6 7 8 9 10 11 12 так расставить во всех промежутках между числами знаки “+” и “–”, чтобы в результате получился 0? |
9 Марта 2004 20:14 | |
17. | Ученики 7 класса решали две задачи. В конце занятия преподаватель составил четыре списка: I –решивших первую задачу, II – решивших только одну задачу, III – решивших по меньшей мере одну задачу, IV – решивших обе задачи. Какой из списков самый длинный? |
9 Марта 2004 20:14 | |
18. | Пусть a, b, c — три цифры, отличные от нуля.
Из них составили шесть различных чисел, в каждом из которых каждая из этих цифр встречается только один раз.
“Крайним” из этих шести чисел называют наибольшее или наименьшее из них.
Число |
9 Марта 2004 20:15 | |
19. | Часы, которые отстают на одну минуту в сутки, в данный момент показывают точное время. Когда они покажут точное время в следующий раз? |
9 Марта 2004 20:16 | |
20. | Даны две параллельные прямые. На каждой прямой отмечено по четыре точки. Сколько можно построить треугольников с вершинами в этих точках? |
9 Марта 2004 20:16 | |
| Страницы: « 1 2 3 » | |
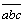 – не “крайнее”.
Укажите еще одно не “крайнее” число. Ответ обоснуйте.
– не “крайнее”.
Укажите еще одно не “крайнее” число. Ответ обоснуйте.