358
471
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2002 года (25)
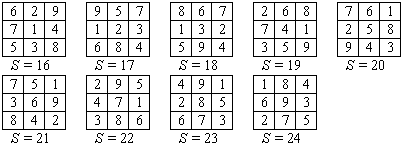
В клетках квадратной таблицы 3 × 3 расставлены числа 1, 2, 3, …, 9 так, что сумма каждых четырех чисел, заполняющих квадрат 2 × 2, равна одному и тому же числу S. Найдите все возможные значения S. |
Ответ: сумма S может принимать все значения от 16 до 24.
Сумма всех этих чисел равна 1 + 2 + … + 9 = 45. Сложим все четыре суммы в квадратах 2 × 2. Получаем
Чтобы S принимала наибольшее значение, надо взять наибольшее значение неизвестных слагаемых, причем то слагаемое, которое употребляется несколько раз, должно быть самым большим. То есть e = 9, b = 8, f = 7, h = 6, d = 5. Тогда 4S = 98. Но 98 не делится на 4. Так как мы брали наибольшие числа, то значение 4S мы не можем увеличить, но зато можем уменьшить до ближайшего числа, делящегося на 4, то есть до 96 и тогда S = 24. Это наибольшее значение, которое может принимать сумма. Аналогично находится наименьшее значение. При e = 1, b = 2, f = 3, h = 4, d = 5 получим 4S = 62, что снова не делится на 4. Надо увеличить эту сумму до ближайшего числа, делящегося на 4, то есть до 64. Тогда S = 16 – наименьшее значение. Ниже представлены все варианты получения сумм от 16 до 26.
|
9 Марта 2004 20:13 Раздел каталога :: Ссылка на задачу
|
Обозначим буквами числа, которые нужно вставить в таблицу (рисунок справа).