358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Осень 2002 года (25)
| Страницы: 1 | |
1. | В распоряжении Кости имеются три банки емкостью 3, 5 и 10 литров. Самая большая банка полностью наполнена водой. Он может переливать воду из одной банки в другую банку следующим образом:
Как Косте отлить из десятилитровой банки в другие банки ровно 4 литра воды? |
9 Марта 2004 20:04 | |
2. | На новогодней распродаже марок в филателистическом магазине любая почтовая марка стоила 1 рубль. При этом к каждым десяти купленным маркам одна давалась бесплатно, а за каждую сотню оплаченных марок еще дарили 5 марок. Заплатив все свои деньги за марки в этом магазине, Денис получил 200 марок. Сколько у него было денег? Ответ пояснить. |
9 Марта 2004 20:04 | |
3. | На дне рождения у Васи каждый мальчик (и Вася тоже!) съел по 4 пирожных и по 3 кекса, а каждая девочка – по одному пирожному и 2 кекса. Оказалось, что число съеденных детьми пирожных равно числу съеденных ими кексов. Кого из гостей было больше на дне рождения у Васи, мальчиков или девочек, и на сколько? Ответ пояснить. |
9 Марта 2004 20:05 | |
4. | Автомат имеет две операции “+5” и “+7”. Сколько различных натуральных чисел можно получить из 1 ровно за 100 операций? Ответ пояснить. |
9 Марта 2004 20:06 | |
5. | Можно ли используя только цифры 7, 8, 9 записать три числа, одно из которых равно произведению двух других? Если можно, приведите пример, в противном случае поясните, почему нельзя. |
9 Марта 2004 20:06 | |
6. | Капитан Врунгель утверждает, что сможет разложить 120 алмазов в отсеки коробки 3 ´ 5 так, чтобы во всех лежало различное число алмазов, а в любых двух соседних (через перегородку) было вместе не более 17 алмазов. Прав ли капитан? (Если прав – приведите пример расположения алмазов, иначе объясните, почему не прав.) |
9 Марта 2004 20:07 | |
7. | У числа можно любую нечетную цифру переставлять в конец (записывать ее справа от него), а любую четную цифру переставлять в начало (записывать ее слева от него). Какое наименьшее число можно получить из числа 391728 такими перестановками? Ответ обоснуйте (то есть докажите, что меньшее число получить нельзя). |
9 Марта 2004 20:08 | |
8. | Бумажный квадрат со стороной 5 см, разрезали на 6 прямоугольников (квадрат также является прямоугольником), с целочисленными периметрами (но не обязательно с целочисленными сторонами). Может ли быть сумма длин их периметров равной 50 см? Целочисленный периметр – это периметр, выраженный целым числом сантиметров. |
9 Марта 2004 20:08 | |
9. | Сколько существует четырехзначных чисел, у которых сумма цифр равна 34? |
9 Марта 2004 20:10 | |
10. | Вчера на базаре Федя купил несколько воздушных шариков – красные по 7 рублей за штуку, а синие по 2 рубля за штуку. Придя сегодня на базар, он обнаружил, что цены шариков поменялись местами: красные стали стоить 2 рубля, а синие 7 рублей. Увидев такое, Федя сказал с досадой: “Покупай я те же шарики сегодня, сэкономил бы 27 рублей”. Докажите, что Федя не прав. |
9 Марта 2004 20:11 | |
11. | Петя и Вася выписывают 12-значное число, ставя цифры по очереди, начиная со старшего разряда. Начинает Вася. Как Пете добиться того, чтобы итоговое число делилось на 9 независимо от ходов Васи? |
9 Марта 2004 20:11 | |
12. | В первенстве по футболу участвует 8 команд. Каждая команда играет с каждой один матч. Команда Меркурий набрала 19 очков, а команда Уран 18. Каков результат матча Меркурий-Уран (ничья, победил Уран, победил Меркурий)? Известно, что за победу присуждается 3 очка, за ничью 1 очко, а за поражение 0 очков. |
9 Марта 2004 20:12 | |
13. | Петя забыл последние 3 цифры телефонного номера, но помнит, что все цифры различны и среди них одна девятка. Какое максимальное число номеров ему придется набрать, чтобы попасть по нужному номеру? |
9 Марта 2004 20:12 | |
14. | В клетках квадратной таблицы 3 × 3 расставлены числа 1, 2, 3, …, 9 так, что сумма каждых четырех чисел, заполняющих квадрат 2 × 2, равна одному и тому же числу S. Найдите все возможные значения S. |
9 Марта 2004 20:13 | |
15. | Масса ста гирек, сваленных в одну кучу, составляет 500 г. Известно, что имеются только гирьки в 1г, 10г, 50г. Сколько в кучке гирек каждой массы? Ответ пояснить. |
9 Марта 2004 20:14 | |
16. | Можно ли в ряду чисел 1 2 3 4 5 6 7 8 9 10 11 12 так расставить во всех промежутках между числами знаки “+” и “–”, чтобы в результате получился 0? |
9 Марта 2004 20:14 | |
17. | Ученики 7 класса решали две задачи. В конце занятия преподаватель составил четыре списка: I –решивших первую задачу, II – решивших только одну задачу, III – решивших по меньшей мере одну задачу, IV – решивших обе задачи. Какой из списков самый длинный? |
9 Марта 2004 20:14 | |
18. | Пусть a, b, c — три цифры, отличные от нуля.
Из них составили шесть различных чисел, в каждом из которых каждая из этих цифр встречается только один раз.
“Крайним” из этих шести чисел называют наибольшее или наименьшее из них.
Число |
9 Марта 2004 20:15 | |
19. | Часы, которые отстают на одну минуту в сутки, в данный момент показывают точное время. Когда они покажут точное время в следующий раз? |
9 Марта 2004 20:16 | |
20. | Даны две параллельные прямые. На каждой прямой отмечено по четыре точки. Сколько можно построить треугольников с вершинами в этих точках? |
9 Марта 2004 20:16 | |
21. | Петя считает пальцы на левой руке от большого до мизинца и обратно от мизинца до большого. Каждый следующий счет приходится на другой палец. На какой палец придется число 1998? |
9 Марта 2004 20:17 | |
22. | Все жители волшебного острова – либо рыцари, говорящие только правду, либо плуты, которые всегда лгут. Посетивший остров мудрец встретил двух жителей, А и Б, и захотел узнать, кто они. Он спросил у А: "Вы оба рыцари?" А ответил. Мудрец понял, что он не может определить, кто такие А и Б, и задал еще один вопрос: "Вы одного типа?" А опять ответил, и мудрец понял, к какому типу относятся А и Б. К какому же? |
9 Марта 2004 20:18 | |
23. | На какое наибольшее число частей могут делить плоскость пять прямых? |
9 Марта 2004 20:50 | |
24. | На празднике конфет можно было обменять любые три фантика на карамельку в фантике, и любые пять фантиков – на шоколадную конфету в фантике. Миша принес на этот праздник 50 конфет. Сможет ли он съесть 5 шоколадных конфет и 15 карамелек? |
9 Марта 2004 20:51 | |
25. | В одной рукописи приведено описание города, расположенного на 8 островах. Острова между собой и с материком соединены мостами. На материк выходят 5 мостов; на четырех островах берут начало по 4 моста; на трех островах берут начало по 3 моста и на один остров можно пройти только по одному мосту. Могут ли так располагаться мосты? |
9 Марта 2004 20:51 | |
| Страницы: 1 | |
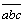 – не “крайнее”.
Укажите еще одно не “крайнее” число. Ответ обоснуйте.
– не “крайнее”.
Укажите еще одно не “крайнее” число. Ответ обоснуйте.