358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Первая лига (8)
| Страницы: 1 | |
1. | Дана замкнутая несамопересекающаяся ломаная с вершинами на ребрах единичного куба. На каждой грани все звенья параллельны между собой. а) Может ли в этой ломаной быть не менее 12 звеньев? б) Может ли длина ломаной быть больше 100? |
27 Февраля 2004 21:04 | |
2. | В каждой клетке прямоугольной доски 26 ´ 77 стоит по фишке.
|
27 Февраля 2004 21:30 | |
3. | Дно коробки 5 ´ 5 выложено квадратными плитками 1 ´ 1, на каждой из которых стоит одна из стрелок ®, ¬, или ¯. За один ход разрешается, выбрав любые две плитки, повернуть одну из них на 90° по часовой, а другую — на 90° против часовой стрелки. Можно ли за несколько ходов придать всем стрелкам направление, противоположное первоначальному? |
28 Февраля 2004 22:20 | |
4. | Можно ли вставить вместо многоточий числа (в десятичной записи) так, чтобы утверждение стало верным: "В этом предложении цифра 0 встречается … раз(а);
|
28 Февраля 2004 22:18 | |
5. | Верно ли, что всякое натуральное число можно представить как разность двух палиндромов? (Палиндромы — это числа, не меняющееся при прочтении справа налево, например, 0, 717, 2002). |
28 Февраля 2004 22:12 | |
6. | Житель страны Ш. считается богатым, если его месячный доход выше зарплаты министра финансов, иначе — небогатым. Известно, что богатые женихи предпочитают небогатых женщин. Докажите, что если доходы у всех разные, то можно установить министру финансов такую зарплату, чтобы в стране стало поровну богатых мужчин и небогатых женщин. |
28 Февраля 2004 22:16 | |
7. | Шулер Фукс кладет даму, короля и туза лицом вниз. Моряк Лом должен не более чем за три попытки разложить их по старшинству слева направо. Перед каждой попыткой он может указать на любые две карты и узнать, какая из них старше. Если после этого он выкладывает карты правильно, Фукс об этом сообщит. Если нет, то перед следующей попыткой Фукс незаметно поменяет местами две соседние карты (при этом он может выложить карты правильно, не сообщая об этом Лому). Есть ли у Лома способ справиться с заданием? |
28 Февраля 2004 22:16 | |
8. | Докажите неравенство |
28 Февраля 2004 22:16 | |
| Страницы: 1 | |
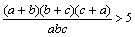 ,
,