358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Первая лига (8)
| Страницы: 1 | |
1. | Целые числа х, у, z таковы, что xy + yz + xz = 1. Докажите, что число (1 + x2)(1 + y2)(1 + z2) является полным квадратом. |
25 Февраля 2004 22:55 | |
2. | Можно ли пятиконечную звездочку разрезать на три выпуклых многоугольника? |
25 Февраля 2004 22:56 | |
3. |
Докажите равенство площадей четырехугольников ALCN и KBMD. |
25 Февраля 2004 22:56 | |
4. | Повар выложил на сковородку восемь котлет по кругу (по часовой стрелке), причем каждая следующая выкладываемая котлета была на 10 граммов тяжелее предыдущей. Когда котлеты поджарились, повар обнаружил, что забыл, с какой котлеты он начинал выкладывать. Помогите ему найти самую тяжелую котлету за два взвешивания на чашечных весах без гирь. |
25 Февраля 2004 22:57 | |
5. | Точку A симметрично отразили относительно четырех прямых. При этом оказалось, что ее образы попали на некоторую окружность с центром O. Затем точку О симметрично отразили относительно тех же прямых. Докажите, что образы точки O принадлежат одной окружности. |
25 Февраля 2004 22:59 | |
6. | Доминошки выкладывают в цепь по следующему правилу: сумма очков на соприкасающихся половинках должна делиться на 8. Какое наибольшее число доминошек может быть в такой цепи? |
25 Февраля 2004 23:01 | |
7. | В серии товарищеских матчей по футболу играют n команд. (Любые две команды встретятся друг с другом ровно по одному разу.) При этом каждая команда в своей k-ой игре забивает k мячей. Составьте расписание так, чтобы как можно меньше игр закончилось вничью. |
25 Февраля 2004 23:00 | |
8. | Положительные числа a, b, c таковы, что a < b < c. Какая из сумм, указанных ниже, ближе к единице:
|
25 Февраля 2004 23:04 | |
| Страницы: 1 | |
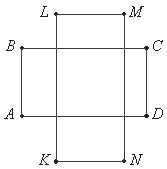 Прямоугольники ABCD и KLMN имеют соответственно параллельные стороны и расположены, как показано на рисунке.
Прямоугольники ABCD и KLMN имеют соответственно параллельные стороны и расположены, как показано на рисунке.
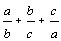 или
или 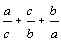 ?
?