358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Командная олимпиада (8)
| Страницы: 1 | |
1. | У завхоза Васи было трое одинаковых чашечных весов. В одних потерялась часть деталей, и теперь они могут показывать что угодно. Любые весы помещаются на одну чашу других весов. За какое наименьшее количество взвешиваний можно определить неисправные весы? |
25 Февраля 2004 22:27 | |
2. | Длины сторон AB и BC треугольника ABC равны 1 и 2 соответственно, ÐABC = 120°. Докажите, что медиана BD перпендикулярна стороне AB. |
25 Февраля 2004 22:28 | |
3. | Двое начинающих играют в крестики-нолики на доске 10 ´ 10. Выигрывает тот, кто поставит три своих значка подряд по вертикали, горизонтали или диагонали. Может ли игра закончиться вничью? |
25 Февраля 2004 22:29 | |
4. | На параде кавалеры ордена Славы выстроились в виде каре 7 ´ 7. У каждого — один, два или три ордена. Дотошные пионеры посчитали число орденов в каждой шеренге, колонне и диагонали из 7 человек. Докажите, что какие-то два из этих чисел совпадают. |
25 Февраля 2004 22:30 | |
5. | На плоскости отметили 8 точек. Каждую пару точек соединили отрезком, затем к каждому такому отрезку построили серединный перпендикуляр. Могло ли на каждом из этих перпендикуляров оказаться ровно по две отмеченные точки? |
25 Февраля 2004 22:30 | |
6. | Найдите все такие тройки простых чисел, что произведение любых двух из них при делении на третье дает остаток 1. |
25 Февраля 2004 22:31 | |
7. |
|
25 Февраля 2004 22:32 | |
8. | Решите систему уравнений:
|
25 Февраля 2004 22:32 | |
| Страницы: 1 | |
 По четырем одинаковым окружностям с центрами в вершинах квадрата (показано на рисунке) с постоянными равными скоростями бегают спортсмены, не переходя с окружности на окружность. Из любых трех спортсменов хотя бы двое иногда встречаются.
По четырем одинаковым окружностям с центрами в вершинах квадрата (показано на рисунке) с постоянными равными скоростями бегают спортсмены, не переходя с окружности на окружность. Из любых трех спортсменов хотя бы двое иногда встречаются.
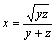 ,
,
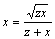 ,
,
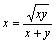 .
.