358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М801 - М820 (20)
| Страницы: « 1 2 | |
11. | M811 Пусть ha, hb, hc — высоты, а ma, mb, mc — медианы остроугольного треугольника (проведенные к сторонам а, b, с), r и R радиусы вписанной и описанной окружностей. Докажите, что
|
28 Января 2004 22:33 | |
12. | M812 Докажите, что при любом натуральном n
|
28 Января 2004 22:35 | |
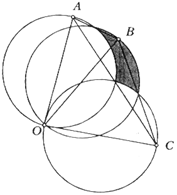
13. | M813
Даны отрезки OА, OB, OС одинаковой длины (точка B лежит внутри угла АОС).
На них как на диаметрах построены окружности.
|
28 Января 2004 22:36 | |
14. | M814 Отметим в натуральном ряду числа, которые можно представить в виде суммы двух квадратов натуральных чисел. Среди отмеченных чисел встречаются тройки последовательных чисел, например 72 = 62 + 62, 73 = 82 + 32, 74 = 72 + 52. а) Объясните, почему не могут встретиться четыре последовательных отмеченных числа. Докажите, что среди отмеченных чисел встретится бесконечно много б) пар, в) троек последовательных чисел. |
28 Января 2004 22:36 | |
15. | M815* На окружности расставлены 4k точек, занумерованных в произвольном порядке числами 1, 2, ..., 4k. а) Докажите, что эти точки можно соединить 2k попарно пересекающимися отрезками так, что разность чисел в концах каждого отрезка не превосходит 3k - 1. б) Постройте пример расстановки номеров, показывающий, что число 3k - 1 в пункте а) нельзя заменить меньшим. |
28 Января 2004 22:37 | |
16. | M816 Натуральные числа a и b получаются друг из друга перестановкой цифр. Докажите, что
|
28 Января 2004 22:38 | |
17. | M817 Точка K лежит на стороне BС треугольника AВС. Докажите, что соотношение AK2 = AB × AC - KB × KC выполнено тогда и только тогда, когда AB = AC или ÐBАK = ÐСАK. |
28 Января 2004 22:39 | |
18. | M818
Пусть какие-то k вершин правильного n-угольника белые (остальные вершины — черные). Будем называть множество белых вершин равномерным, если при любом m количества белых вершин в любых двух наборах из m последовательных вершин n-угольника совпадают или отличаются на 1 (см. рисунок, где приведен пример равномерного множества для n = 8, k = 5). а) Постройте равномерные множества для
n = 12, k = 5;
Докажите, что равномерное множество существует и единственно (с точностью до поворотов n-угольника), б) если n делится на k; в)* для любых n и k (k £ n). |
28 Января 2004 22:40 | |
19. | M819 В Швамбрании n городов, каждые два из которых соединены дорогой. (Дороги сходятся лишь в городах, все пересечения организованы в разных уровнях.) Злой волшебник намеревается установить на каждой дороге одностороннее движение так, что выехав из любого города, в него уже нельзя будет вернуться. Докажите, что а) волшебник может это сделать; б) при этом найдется город, из которого можно добраться до всех других, и найдется город, из которого нельзя выехать; в) существует n! = 1 × 2 × ... × n способов осуществить намерение злого волшебника. |
28 Января 2004 22:41 | |
20. | M820* а) Правильный восьмиугольник разрезан на конечное число параллелограммов.
б) Правильный 4k-угольник разрезан на конечное число параллелограммов.
в) Найдите суммарную площадь прямоугольников из пункта б), если длина стороны 4k-угольника равна 1. |
28 Января 2004 22:42 | |
| Страницы: « 1 2 | |
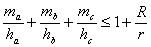 .
.
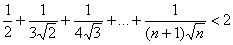 .
.