358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M781 - M800 (20)
| Страницы: « 1 2 3 4 | |
16. | M796 Точка P расположена внутри квадрата АВСD так, что AP : BP : CP = 1 : 2 : 3. Найдите ÐАРВ. |
27 Января 2004 22:27 | |
17. | M797* Известно, что последними цифрами квадратов целых чисел могут быть лишь цифры 0, 1, 4, 5, 6 и 9. Верно ли, что перед последней цифрой в них может встретиться любая группа цифр, т.е. что для любого набора из n цифр a1, a2,..., an можно найти целое число, квадрат которого оканчивается цифрами a1a2anb, где b — одна из перечисленных выше цифр? |
27 Января 2004 22:29 | |
18. | M798* На окружности отметили 4k точек и раскрасили их попеременно в красный и синий цвета; затем 2k красных точек произвольным образом соединили попарно k красными отрезками, а 2k синих — k синими отрезками (никакие три отрезка не пересекаются в одной точке). Докажите, что найдется по крайней мере k точек пересечения красных отрезков с синими. |
27 Января 2004 22:29 | |
19. | M799 а) Найдите одно решение уравнения 3x+1 + 100 = 7x-1 и докажите, что у него нет других решений. б) Найдите два решения уравнения 3x + 3x2 = 2x + 4x2 и докажите, что у него нет других решений. |
27 Января 2004 22:30 | |
20. | M800*
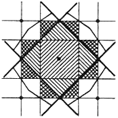
а) На плоскости отмечены все точки с целочисленными координатами — узлы квадратной решетки, и среди них выделен один «начальный» узел O. Для каждого из остальных узлов P проведена прямая, относительно которой узлы O и P симметричны, — серединный перпендикуляр к отрезку OP. Проведенные прямые разбивают плоскость на мелкие части (треугольники и выпуклые многоугольники). Припишем каждой из них натуральное число — ранг — по следующему правилу: часть, содержащая точку O (она имеет форму квадрата), получает ранг 1, части, граничащие с ней по стороне, — ранг 2, части, граничащие с ними по стороне (и отличные от уже рассмотренных) — ранг 3 и т. д. (показано на рисунке). Докажите, что суммарная площадь всех частей ранга r одна и та же при всех натуральных r. б) Верно ли аналогичное утверждение для произвольной решетки из параллелограммов (в частности, из ромбов с углом в 60°)? Для решетки из правильных шестиугольников? в) Сформулируйте и докажите аналогичное утверждение для кубической решетки в пространстве. |
27 Января 2004 22:31 | |
| Страницы: « 1 2 3 4 | |