358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
M781 - M800 (20)
| Страницы: 1 | |
1. | M781 Постройте прямую, параллельную стороне АС данного треугольника ABC и пересекающую его стороны АВ и ВС в таких точках D и Е соответственно, что AD = BE. |
27 Января 2004 21:35 | |
2. | M782 Докажите, что если сумма двух натуральных чисел равна 30030, то их произведение не делится на 30030. |
27 Января 2004 21:36 | |
3. | M783 а) При каком наибольшем n система неравенств б) Для каких n существуют такие две прогрессии — арифметическая
a1, a2, a3,..., an+1
и геометрическая b1, b2, b3,..., bn, что |
27 Января 2004 21:37 | |
4. | M784 Шарообразная планета движется по окружности вокруг звезды и вращается вокруг своей оси, причем ось суточного вращения наклонена к плоскости орбиты под углом α (для нашей Земли α = 66,5°). Найдите зависимость продолжительности Т самого короткого дня в году в данном пункте на поверхности планеты от географической широты φ этого пункта. (Угловая скорость вращения планеты по орбите много меньше угловой скорости вращения планеты вокруг ее оси.) Напишите формулу для функции Т = Т(φ) и начертите примерный график. |
27 Января 2004 21:38 | |
5. | M785 a) Про возрастающую последовательность положительных чисел a(n), n = 1, 2, 3,..., известно, что для любого натурального числа k > 1 существует число bk такое, что a(kn) £ bka(n) при всех n. Докажите, что существуют положительные числа c и α, для которых a(n) £ cnα при всех n ³ 1. Останется ли верным это утверждение, если в условии б) слово «любого» заменить на «некоторого»? в) не требовать, чтобы последовательность a(n) была возрастающей? |
27 Января 2004 21:39 | |
6. | M786 Докажите, что для любых натуральных k и n (больших 1) число nk можно представить в виде суммы k последовательных нечетных чисел. (Например, 43 = 13 + 15 + 17 + 19; 72 = 1 + 3 + 5 + 7 + 9 + 11 + 13; 34 = 25 + 27 + 29.) |
27 Января 2004 21:40 | |
7. | M787 Найдите отношение сторон прямоугольного треугольника, если известно, что одна половина гипотенузы (от вершины до середины гипотенузы) видна из центра вписанной окружности под прямым углом. |
27 Января 2004 21:41 | |
8. | M788 а) На графике y = x2 отмечены точки A(a; b2) и B(b; b2). Найдите между ними точку M(m; m2), для которой сумма площадей двух сегментов, ограниченных графиком и отрезками AM и BM, наименьшая. б) На графике дифференцируемой функции y = f(x) отмечены точки А и В. Известно, что график и отрезок АВ ограничивают выпуклую фигуру. Пусть M — точка графика, расположенная между А и B, для которой сумма площадей двух сегментов, ограниченных графиком и отрезками AM и BM, наименьшая. Докажите, что касательная к графику в точке M параллельна хорде АB. |
27 Января 2004 21:42 | |
9. | M789 а) 10 точек, делящие окружность на 10 равных дуг, попарно соединены пятью хордами. Обязательно ли среди них найдутся хорды одинаковой длины? б)* 100 точек, делящие окружность на 100 равных дуг, попарно соединены 50 хордами. Докажите, что среди них обязательно найдутся две хорды одинаковой длины. |
27 Января 2004 21:42 | |
10. | M790 а) Про числовую функцию f известно, что если
Пусть про отображение F плоскости в себя известно, что любые две точки X, Y,
находящиеся на расстоянии 1, оно переводит в две точки
Тогда для любых двух точек X, Y плоскости
б) ρ(F(X),F(Y)) £ ρ(X, Y) + 1; в)* ρ(X, Y) = г)* ρ(F(X),F(Y)) £ ρ(X, Y);; д)* ρ(F(X),F(Y)) ³ ρ(X, Y);. (Вы можете, конечно, предложить и другой план доказательства теоремы.) |
27 Января 2004 21:44 | |
11. | M791 Пете подарили микрокалькулятор, на котором можно выполнять следующие операции: по любым данным числам x и y вычислить x + y, x + y, x + 1 и 1/x (при x ¹ 0). Петя утверждает, что с помощью своего микрокалькулятора он может: а) возвести любое число в квадрат, проделав не более шести операций; б)* перемножить любые два числа, проделав не более двадцати операций. Как он это делает? |
27 Января 2004 21:45 | |
12. | M792 Решите в натуральных числах уравнения а) 3x + 1 = 2y; б) 3x - 1 = 2y. в)* Найдите все натуральные n, при которых оба числа 1/n и г) Докажите, что при любом простом p > 3 и натуральном m > 1 ни одно из чисел pm + 1 и pm - 1 не может быть степенью двойки. |
27 Января 2004 21:46 | |
13. | M793*
Из вершины P тетраэдра PАВС проводятся три отрезка PA', PB', PC', перпендикулярные граням PВС, PСА, PАВ и равные по длине площадям этих граней соответственно (направления отрезков выбираются так, что точки A' и А, B' и B, C' и С лежат по разные стороны плоскостей соответствующих граней PВС, PСА, PАВ (показано на рисунке). Докажите, что а) повторив это же построение для тетраэдра (и его вершины P), мы получим тетраэдр, гомотетичный исходному тетраэдру PАВС с коэффициентом 3V/4, где V равно объему тетраэдра PАВС; б) вектор в) Из точки O, взятой внутри тетраэдра АВСD, опускаются перпендикуляры на плоскости его граней. На этих перпендикулярах от точки O откладываются отрезки, равные по длине площадям соответствующих граней, и концы этих отрезков принимаются за вершины нового тетраэдра А'В'С'D'. (Разумеется, с точностью до параллельного переноса, этот тетраэдр не зависит от выбора точки O.) Докажите, что, повторив это построение для тетраэдра А'В'С'D', мы получим тетраэдр, гомотетичный исходному с коэффициентом 3V, где V — объем исходного тетраэдра АВСD. (Если 3V = 1, то последний тетраэдр получается из исходного параллельным переносом.) |
27 Января 2004 22:24 | |
14. | M794
Две окружности пересекаются в точках А и B. Через точку K первой окружности проведены прямые KА и KВ, пересекающие вторую окружность в точках P и Q (показано на рисунке). Докажите, что хорда PQ второй окружности перпендикулярна диаметру KM первой окружности. |
27 Января 2004 21:49 | |
15. | M795 Обозначим через σ(n) все делители натурального числа n (см. таблицу). а) σ(n) > 2n; б) σ(n) > 3n. Докажите, что для любого n в) σ(n) < n(log2 n + 2); г) σ(n) < n(ln n + 1). |
27 Января 2004 21:50 | |
16. | M796 Точка P расположена внутри квадрата АВСD так, что AP : BP : CP = 1 : 2 : 3. Найдите ÐАРВ. |
27 Января 2004 22:27 | |
17. | M797* Известно, что последними цифрами квадратов целых чисел могут быть лишь цифры 0, 1, 4, 5, 6 и 9. Верно ли, что перед последней цифрой в них может встретиться любая группа цифр, т.е. что для любого набора из n цифр a1, a2,..., an можно найти целое число, квадрат которого оканчивается цифрами a1a2anb, где b — одна из перечисленных выше цифр? |
27 Января 2004 22:29 | |
18. | M798* На окружности отметили 4k точек и раскрасили их попеременно в красный и синий цвета; затем 2k красных точек произвольным образом соединили попарно k красными отрезками, а 2k синих — k синими отрезками (никакие три отрезка не пересекаются в одной точке). Докажите, что найдется по крайней мере k точек пересечения красных отрезков с синими. |
27 Января 2004 22:29 | |
19. | M799 а) Найдите одно решение уравнения 3x+1 + 100 = 7x-1 и докажите, что у него нет других решений. б) Найдите два решения уравнения 3x + 3x2 = 2x + 4x2 и докажите, что у него нет других решений. |
27 Января 2004 22:30 | |
20. | M800*
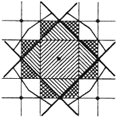
а) На плоскости отмечены все точки с целочисленными координатами — узлы квадратной решетки, и среди них выделен один «начальный» узел O. Для каждого из остальных узлов P проведена прямая, относительно которой узлы O и P симметричны, — серединный перпендикуляр к отрезку OP. Проведенные прямые разбивают плоскость на мелкие части (треугольники и выпуклые многоугольники). Припишем каждой из них натуральное число — ранг — по следующему правилу: часть, содержащая точку O (она имеет форму квадрата), получает ранг 1, части, граничащие с ней по стороне, — ранг 2, части, граничащие с ними по стороне (и отличные от уже рассмотренных) — ранг 3 и т. д. (показано на рисунке). Докажите, что суммарная площадь всех частей ранга r одна и та же при всех натуральных r. б) Верно ли аналогичное утверждение для произвольной решетки из параллелограммов (в частности, из ромбов с углом в 60°)? Для решетки из правильных шестиугольников? в) Сформулируйте и докажите аналогичное утверждение для кубической решетки в пространстве. |
27 Января 2004 22:31 | |
| Страницы: 1 | |

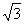 ;
Þ
ρ(F(X),F(Y)) =
;
Þ
ρ(F(X),F(Y)) = 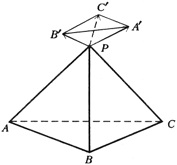
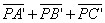 перпендикулярен плоскости АВС.
перпендикулярен плоскости АВС.