358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
М761 - М780 (20)
| Страницы: « 1 2 | |
11. | M771 В треугольнике АВС проведена биссектриса АK. Известно, что центры окружностей: вписанной в треугольник АВK и описанной около треугольника АВС — совпадают. Найдите углы треугольника АВС. |
18 Января 2004 21:41 | |
12. | M772 В мастерской имеется пять различных станков. Обучение одного рабочего работе на одном станке стоит 1000 рублей. С какими наименьшими затратами можно обучить 8 рабочих так, чтобы при отсутствии любых трех из них все станки могли быть одновременно использованы в работе? Каждый рабочий может одновременно работать только на одном станке. |
18 Января 2004 21:43 | |
13. | M773 Окружность, вписанная в треугольник АВС, касается его сторон АВ, ВС и АС
в точках M, N и P соответственно.
Известно, что
|
18 Января 2004 21:43 | |
14. | M774 Функция f(x), определенная на отрезке [0; 1], такова, что (1) f(0) = f(1) = 0 и (2) для всех а) f(x) ³ 0 при всех x Î [0; 1]; б) f(x) имеет бесконечно много нулей на отрезке [0; 1]; в) если существует такое число А ³ 0, что для всех x Î [0; 1/2] выполнено неравенство f(x) £ А, то f(x) £ А для каждого x Î [0; 1]; г)* если функция f(x) непрерывна хотя бы в одной точке x0 отрезка [0; 1], то f(x) = 0 для всех x Î [0; 1]; д)* существуют функции f(x), удовлетворяющие условиям (1), (2), не равные тождественно нулю. |
18 Января 2004 21:45 | |
15. | M775 При каких натуральных n ³ 3 существуют различные натуральные числа a1, a2, ..., an такие, что 1 £ ak £ n + 1 для любого k = 1, 2, ..., n и все n чисел ½a1 - a2½, ½a2 - a3½, ..., ½an-1 - an½, ½an - a1½ различны? |
18 Января 2004 21:46 | |
16. | M776 На диагоналях АС и СЕ правильного шестиугольника АВСDЕF взяты точки
M и N соответственно, такие что
Известно, что точки B, M, N лежат на одной прямой. Найдите λ. |
18 Января 2004 21:47 | |
17. | M777 Дано уравнение x3 - xy2 + y3 = n. Докажите, что а) если натуральное n таково, что данное уравнение имеет целочисленное решение, то оно имеет по крайней мере три целочисленных решения; б) при n = 2891 это уравнение не имеет целочисленных решений. |
18 Января 2004 21:48 | |
18. | M778* Дан неравнобедренный треугольник A1A2A3. Пусть ai — его сторона, лежащая против вершины Ai (i = 1, 2, 3), Mi — середина стороны , Ti — точка касания стороны с окружностью, вписанной в данный треугольник, и Si — точка, симметричная Ti относительно биссектрисы угла Ai треугольника. Докажите, что прямые M1S1, M2S2 и M3S3 имеют общую точку. |
18 Января 2004 21:49 | |
19. | M779* Рассматриваются последовательности (xn) положительных чисел, удовлетворяющие условию а) Докажите, что для любой такой последовательности (xn) существует n, при котором
б) Найдите такую последовательность (xn), удовлетворяющую указанному условию, для которой при любом n
|
18 Января 2004 21:49 | |
20. | M780* Дан квадрат K со стороной 100. Пусть L — несамопересекающаяся незамкнутая ломаная, лежащая в K, такая, что для любой точки Р границы квадрата K найдется точка ломаной L, расстояние которой от Р не больше 1/2. Докажите, что на ломаной найдутся две точки X и Y, расстояние между которыми не более 1, такие, что длина части ломаной, заключенной между ними, не меньше 198. |
18 Января 2004 21:50 | |
| Страницы: « 1 2 | |
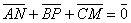 .
Докажите, что треугольник
АВС — правильный.
.
Докажите, что треугольник
АВС — правильный.
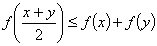
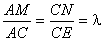 .
.
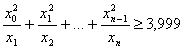 .
.
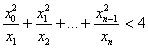 .
.