Финальный тур боев (13)

1.

Существуют ли 5 различных натуральных чисел, наименьшее общее кратное которых равно 5m, где m — наименьшее из чисел?

2.

В газете написали, что в парламенте Ругандии очередной раз поругались все 1998 депутатов, после чего отправили друг другу письма с обвинениями. По утверждению журналиста, все депутаты отправили писем поровну, и никакие два депутата письмами не обменялись, хотя и из любых двух депутатов один отправил другому письмо. Докажите, что журналист ошибается.

3.

Можно ли на плоскости отметить 9 точек так, чтобы нашлось 13 прямых, на каждой из которых лежит ровно 3 из отмеченных точек?

4.

Из 27 игральных кубиков (грани каждого занумерованы числами 1, 2, ..., 6 так, что сумма номеров противоположных граней равна 7) сложили куб. При этом соседние кубики граничат по граням с одинаковыми номерами. Какова может быть сумма номеров на поверхности получившегося куба?

5.

Какое наибольшее число ладей можно поставить на шахматную доску, чтобы среди них только две били друг друга?

6.

Из набора гирек массой 1, 2, 3, ..., 101 г потерялась гирька массой 19 г. Можно ли оставшиеся 100 гирек разложить на две кучки по 50 гирек в каждой так, чтобы массы гирек обеих кучек были одинаковыми?

7.

Каждая из клеток квадрата 5 ´  5 покрашена в один из четырех цветов так, что в любом квадрате 2 ´  2 встречаются все 4 цвета. Какое наибольшее число клеток при этом может быть окрашено в один цвет?

8.

Может ли устроить однокруговой футбольный турнир 13 команд так, чтобы каждая команда сыграла дома нечетное число матчей? (Считается, что в каждом матче одна команда играет дома, а вторая — в гостях).

9.

Имеется 9 чисел: –6, –4, –2, –1, 1, 2, 3, 4, 6. Двое играют в следующую игру: один ищет наборы чисел, сумма которых равняется –8, а другой — наборы с суммой 11. Выигрывает тот, у кого найдется меньше наборов. Может ли кто-то выиграть в этой игре?

10.

Количество мальчиков, решивших на уроке сложную задачу, больше количества девочек, ее не решивших. Кого больше: тех, кто решил сложную задачу, или девочек?

11.

Хулиганы Вася и Петя по очереди (начиная с Васи) вырывают из книги по одному листу. Всего в этой книге 50 листов, а страницы пронумерованы последовательно от 1 до 100. Тот мальчик, у которого сумма номеров каких-либо (возможно не всех) вырванных им страниц окажется равной 100, выигрывает, и игра останавливается. Но при этом Вася может суммировать только нечетные, а Петя — только четные номера страниц. Может ли Петя играть так, чтобы всегда выигрывать?

12.

Можно ли в 12-угольнике провести некоторые диагонали так, чтобы из каждой вершины выходило ровно 5 диагоналей?

13.

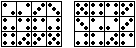В таблице разрешается переставлять местами любые две строки и любые два столбца. Можно ли из левой таблицы в результате нескольких таких преобразований получить правую таблицу?