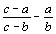358
470
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 5 (8)
| Страницы: 1 | |
1. | На территории завода четыре асфальтовые дорожки длиной 10 м каждая образуют квадрат. В двух соседних вершинах квадрата стоят двое рабочих, держа на плечах десятиметровую трубу. Им необходимо, передвигаясь по дорожкам и не выпуская при этом трубы, поменяться местами. Из соображений безопасности разрешается идти со скоростью не больше 1 м/с. За какое наименьшее время рабочие могут справиться с заданием? (Внутри квадрата нет никаких сооружений, создающих помехи при переноске трубы). |
11 Ноября 2003 18:10 | |
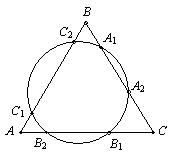
2. |
Окружность пересекает стороны равностороннего треугольника в шести точках, как показано на рисунке. Докажите, что AB2 + CA2 + BC2 = AC1 + BA1 + CB1. |
11 Ноября 2003 18:11 | |
3. | Докажите, что ни при каких целых a, b и c числа
не могут быть целыми одновременно. |
11 Ноября 2003 18:12 | |
4. | Разрежьте квадрат на шесть частей так, чтобы ими можно было полностью и без перекрытий оклеить поверхность некоторого куба. |
11 Ноября 2003 18:13 | |
5. | Натуральное число назовем удобным, если его можно представить в виде суммы двух натуральных слагаемых, суммы цифр которых одинаковы. Докажите, что существуют 1000000 последовательных натуральных чисел, являющихся удобными. |
11 Ноября 2003 18:14 | |
6. | Рассмотрим множество всех квадратных таблиц p ´ p клеток (p > 1), заполненных натуральными числами 1, 2, …, p2. Пусть A — подмножество, в котором каждую таблицу можно получить из правильной операциями перестановки столбцов и перестановки строк (правильная таблица — таблица, в которой в первой строке (столбце) стоят по порядку числа 1, 2, …, p, во второй строке (столбце) — p + 1, p + 2, …, 2p, и так далее); B — подмножество, в котором из любой таблицы можно получить таблицу с равными числами операциями прибавления числа 1 ко всем числам строки или столбца. Докажите, что A = B тогда и только тогда, когда p — простое. |
11 Ноября 2003 18:15 | |
7. |
В середине одной из стен квадратной комнаты 3 ´ 3 имеется проход шириной 1 (показано на рисунке). Можно ли в эту комнату внести какой-нибудь стол, имеющий площадь более 4? |
11 Ноября 2003 18:30 | |
8. | Пусть [a, b, c] — наименьшее общее кратное натуральных чисел a, b и c. Может ли для каких-нибудь x, y и z оказаться, что [x, y, z] = [x + 1, y + 1, z + 1] = [x + 2, y + 2, z + 2]? |
11 Ноября 2003 18:31 | |
| Страницы: 1 | |
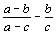 ,
, 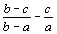 ,
,