Вариант боев 4 (10)

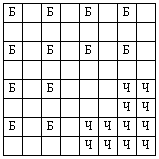
Ответ: 12 королей.

Решение. Пусть на доске уже расставлено несколько королей с соблюдением указанных условий. Будем считать белыми королей, которые никому не угрожают (значит, и им никто не угрожает), а черными — королей, которые кому-то угрожают (следовательно, им угрожают только другие черные короли).

Заметим, что можно расставить 24 короля (по 12 каждого цвета); один из способов (здесь белые и черные короли обозначены буквами “Б” и “Ч” соответственно) показан на рисунке.

Докажем, что число королей каждого цвета не может превышать 12.

Допустим обратное — что королей каждого цвета может быть не меньше 13. Разобьем доску на 16 квадратов размером 2 ´ 2. Заметим, что в каждом квадрате может стоять не более одного белого короля (иначе какие-то два из них будут угрожать друг другу). При этом если в квадрате стоит белый король, то ни одного черного короля в этом же квадрате быть не может.

Если в шестнадцати квадратах 2 ´ 2 содержится в общей сложности не менее 13 белых королей, причем в каждом квадрате — не более одного короля, то квадратов, не содержащих белых королей, не более 3. В каждом из таких “свободных” квадратов может находиться не более четырех черных королей, а всего — не более 4 × 3 = 12, а должно быть не меньше 13. Противоречие. Следовательно, предположение было неверным, и расставить больше 12 королей каждого цвета нельзя.

Автор задачи — И. Акулич