358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 4 (10)
Задачи 32-39 составили боле сложный вариант, задачи 32, 33, 35, 37-41 составили менее сложный вариант
В трапеции ABCD основание BC вдвое меньше AD; DD1 — перпендикуляр, опущенный на прямую AB. Докажите, что если окружность, описанная около треугольника BCD1, касается стороны AD, то трапеция — равнобокая. |
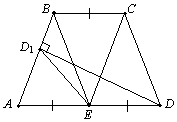
Решение. Пусть точка E — середина стороны AD (показано на рисунке). Тогда AE = D1E (так как медиана прямоугольного треугольника ADD1, проведенная к гипотенузе, равна ее половине), откуда ÐAD1E = ÐBAD. Так как BC = AE = ED, то ABCE — параллелограмм, откуда следует, что ÐCED1 = ÐAD1E = ÐBAD = 180° – ÐABC. Значит, точки B, C, D1 и E лежат на одной окружности, которая описана около треугольника BCD1 и касается стороны AD. То есть точка E — точка касания окружности. Отсюда следуют равенство ÐCBE = ÐAEB = ÐBCE = ÐBAE = ÐCDA, значит, данная трапеция — равнобокая. |
Автор задачи — Д. Калинин Дополнение. Для треугольника, образованного прямыми AB, CD и DA, отрезок BC является средней линией, отрезок DD1 — высотой, поэтому окружность, указанная в задаче, — окружность девяти точек этого треугольника. Раз она касается стороны AD, то основание высоты и медианы, опущенных на эту сторону, совпадают, следовательно, треугольник — равнобедренный, а наша трапеция — равнобокая. |
11 Ноября 2003 18:01 Раздел каталога :: Ссылка на задачу
|