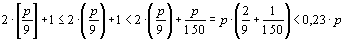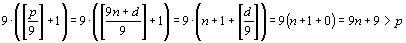Вариант боев 4 (10)

Решение. Докажем более сильное утверждение: что существует палиндром, содержащий не более 2 × [p / 9] + 1 цифр (здесь квадратные скобки обозначают целую часть). То, что это действительно более сильное утверждение, доказывает следующая цепочка неравенств:

А теперь возьмем для начала (2 × [p / 9] + 1)-значное число, у которого первая и последняя цифры — единицы, а все остальные (“внутренние”) — нули. Под ним запишем второе число, у которого первая и последняя цифры — двойки (а прочие остаются нулями). Затем запишем третье число, у которого крайние цифры — тройки и так далее вплоть до девяток. Теперь займемся таким же “увеличением” от 0 до 9 двух других цифр — второй слева и второй справа, не трогая остальных. Затем увеличиваем третью слева и третью справа цифры и так далее, вплоть до [p / 9]-й цифры слева и [p / 9]-й цифры справа. Последнее выписанное число состоит только из девяток, за исключением средней цифры, равной 0. Наконец, последнее действие: постепенно увеличиваем от 0 до 9 эту среднюю цифру, пока все цифры числа не станут равными 9. “Общий вид” этого списка чисел показан на рисунке.

Всего было выписано столько чисел, сколько раз нам приходилось увеличивать на 1 очередную пару цифр или (на последнем этапе) единственную среднюю цифру. Это равно 9 × ([p / 9] + 1), что не меньше числа р. В самом деле, если р = 9n + d, где 0 £ d < 9, то

Заметим также, что все выписанные числа — палиндромы. Если какой-то из них делится на р, то все в порядке — указанный в условии палиндром существует. Если же нет, то найдутся два палиндрома, дающие одинаковые остатки при делении на р (поскольку всего палиндромов не меньше р). Вычтем из большего палиндрома меньший, их разность будет делиться на число р. Так как каждая цифра большего палиндрома не меньше соответствующей цифры меньшего палиндрома, то разность станет палиндромом (возможно с приписанными в конце нулями). Отбросив нули в конце (это никак не влияет на делимость числа на простое число p > 150), получим искомый палиндром.

Автор задачи — И. Акулич

Отметим, что то же верно не только для простых р, но и для любых натуральных р, не делящихся ни на 2, ни на 5.