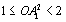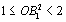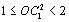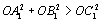358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 4 (10)
Задачи 32-39 составили боле сложный вариант, задачи 32, 33, 35, 37-41 составили менее сложный вариант
Биссектрисы АА1, ВВ1, СС1 остроугольного треугольника АВС пересекаются в точке О. Докажите, что из отрезков ОА1, ОВ1, ОС1 можно составить остроугольный треугольник. |
Решение. В остроугольном треугольнике любой угол между стороной и проведенной к ней биссектрисой больше 45°. Действительно, рассматривая, например, угол АА1В как внешний угол треугольника АА1С, получим
Теперь заметим, что если ОР — перпендикуляр, опущенный на ВС, то
В самом деле, в случае совпадения точек А1 и Р эти неравенства очевидны, а в случае несовпадения имеем прямоугольный треугольник ОА1Р, в котором ОА1 — гипотенуза, а ОР — катет, лежащий против угла, большего 45°. Длина перпендикуляра, опущенного из точки O на любую из сторон, равна радиусу окружности, вписанной в треугольник АВС; примем этот радиус за 1. Из доказанного выше следуют неравенства
Из них следует, что Значит, из отрезков ОА1, ОВ1, OC1 можно составить треугольник. Из тех же неравенств следует, что
откуда получается, что
Эти неравенства гарантируют, что получившийся треугольник — остроугольный. |
Автор задачи — С. Токарев |
11 Ноября 2003 17:56 Раздел каталога :: Ссылка на задачу
|
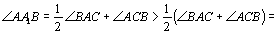
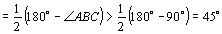
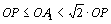
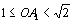
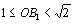
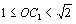 .
.