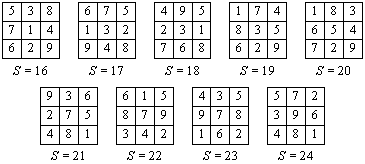358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Вариант боев 1 (8)
В клетках квадратной таблицы 3 ´ 3 расставлены числа 1, 2, 3, …, 9 так, что сумма каждых четырех чисел, заполняющих квадрат 2 ´ 2, равна одному и тому же числу S. Найдите все возможные значения S. |
Ответ: 16, 17, …, 24.
Решение. Пусть таблица имеет вид, показанный на рисунке, где a, b, …, i — числа 1, 2, …, 9. Так как a + c + g + i ³ 1 + 2 + 3 + 4 = 10, то выполнено, по крайней мере, одно из неравенств a + i ³ 5 и c + g ³ 5; пусть, для определенности, c + g ³ 5. Из соотношения 2S = (a + b + d + e) + (e + f + h + i) = (a + b + с + d + e + f + g + h + i) + e – c – g следует, что 2S = 45 + e – c – g, откуда 2S £ 45 + 9 – 5 = 49, так как e £ 9, c + g ³ 5. Поэтому число S, будучи целым, не превосходит 24. Аналогично, используя неравенство a + c + g + i £ 6 + 7 + 8 + 9 и полагая, что с + g £ 15, получаем оценку 2S ³ 45 + 1 – 15, откуда S ³ 16. На рисунке показано, что S может равняться любому целому числу от 16 до 24.
|
Автор задачи — В.Замков, г.Липецк |
10 Ноября 2003 21:55 Раздел каталога :: Ссылка на задачу
|