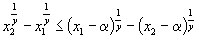Финал (10)

1.

В квадрате n ´ n стоят ненулевые числа. Известно, что каждое число ровно в k раз меньше, чем сумма всех чисел, стоящих с ним в одном "кресте" (то есть в одной строке или в одном столбце, кроме него самого). При каких k это возможно?

2.

На доске написаны числа 1, 2, …, 1999. Два игрока по очереди делают ходы по следующим правилам: при каждом ходе разрешается стереть любые два числа и записать на их место либо их сумму, либо их произведение, либо разность (любого знака). Первый игрок хочет, чтобы число, которое останется на доске последним, делилось на 1999. Сможет ли второй ему помешать?

3.

Окружности S₁ и S₂ пересекаются в точках A и B. Окружность S₃ касается внешним образом S₁ и S₂ в точках C и D соответственно. Пусть PQ — хорда, высекаемая прямой AB на окружности S₃, а K — середина CD. Докажите равенство углов PKC и QKC.

4.

Докажите, что для каждого унитарного многочлена f (x) десятой степени с целыми коэффициентами найдутся два различных натуральных числа a и b, не превосходящие 101, для которых f (a) – f (b) делится на 101.

5.

На плоскости проведено 500 прямых. Оказалось, что среди любых семи из этих прямых какие-то три проходят через одну точку, причем ни через какую точку не проходит более 500 прямых. Докажите, что на плоскости можно отметить 3 точки так, что каждая из прямых будет проходить через одну из отмеченных точек.

6.

Докажите, что в графе с N вершинами, степень любой вершины которого не менее трех, существует остовное дерево, в котором более чем 2N / 9 висячих вершин.

7.

В четырехугольнике ABCD лежат две окружности радиусов R₁ и R₂, касающиеся внешним образом. Первая окружность касается сторон DA, AB и BC, причем стороны AB в точке E.
Вторая окружность касается сторон BC, CD и DA, причем стороны CD в точке F. Диагонали четырехугольника пересекаются в точке O. Докажите, что OE + OF £ 2(R₁ + R₂).

8.

В клетках бесконечного клетчатого листа расставлены целые числа таким образом, что для каждого числа a сумма двух чисел в клетках под ним и справа от него равна 2a + 1. Докажите, что в каждом бесконечном диагональном ряду направления "сверху справа вниз влево" все числа различны.

9.

Пусть d = НОД (a, b) и a = a'd, b = b'd, n — натуральное число, большее 1. Докажите, что если b' — четно, то НОД (n^a + 1, n^b – 1) £ 2.

10.

Пусть 0 £ a £ x₁ £ x₂ и y > 1. Докажите неравенство: