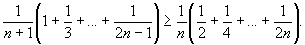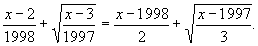358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/2 финала. Вариант 2 (10)
| Страницы: 1 | |
1. | Из каждой вершины (не обязательно выпуклого) многоугольника можно провести диагональ длины, не превосходящей 1, целиком лежащую внутри многоугольника. Докажите, что у этого многоугольника найдется сторона, длина которой не превосходит 1. |
16 Апреля 2004 21:33 | |
2. | Пусть n - натуральное число, большее 1. Докажите, что
|
16 Апреля 2004 21:33 | |
3. | Отрезок железной дороги между городами A и K имеет длину 56 км. Поезд делает на нем 9 промежуточных остановок — на станциях B, C, D, E, F, G, H, I и J. Известно, что длина любых двух соседних участков дороги не превосходит 12 км, а длина любых трех подряд идущих участков дороги не меньше 17 км. Найдите расстояние между станциями B и G. |
16 Апреля 2004 21:34 | |
4. | Докажите, что сумма квадратов всех делителей натурального числа n (включая 1 и n) не может равняться (n + 1)2. |
16 Апреля 2004 21:34 | |
5. | Таблица m ´ n (m, n ³ 3) заполнена числами так, что числа в каждом столбце образуют арифметическую прогрессию. Какие-то две строки этой таблицы также являются арифметическими прогрессиями. Докажите, что и в остальных строках таблицы тоже записаны арифметические прогрессии. |
16 Апреля 2004 21:35 | |
6. | Про натуральные числа x, y и z известно, что (z + 1)x2 + x = zy2 + y. Докажите, что число (y – x) является точным квадратом. |
16 Апреля 2004 21:35 | |
7. | Решите уравнение:
|
16 Апреля 2004 21:35 | |
8. | Восемь шахматистов сыграли турнир в один круг. Известно, что в любой тройке шахматистов были двое, сыгравшие между собой вничью. Какое наименьшее число ничьих могло быть в этом турнире? |
16 Апреля 2004 21:36 | |
9. | В квадрат вписан четырехугольник P (на каждой стороне квадрата по одной вершине четырехугольника), в который в свою очередь вписали квадрат (также на каждой стороне четырехугольника по одной вершине квадрата), причем все 12 вершин этих четырехугольников различны. Могло ли так получиться, что у четырехугольника P все стороны попарно различны? |
16 Апреля 2004 21:36 | |
10. | Точка O — центр описанной окружности треугольника ABC; лучи AO и CO вторично пересекают описанную окружность соответственно в точках D и E таких, что ÐDEC = ÐDAB и ÐEDA = ÐECB. Докажите, что треугольник ABC равносторонний. |
16 Апреля 2004 21:36 | |
| Страницы: 1 | |