358
473
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/2 финала. Вариант 2 (10)
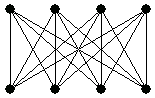
Восемь шахматистов сыграли турнир в один круг. Известно, что в любой тройке шахматистов были двое, сыгравшие между собой вничью. Какое наименьшее число ничьих могло быть в этом турнире? |
Будем вершинами графа обозначать шахматистов, а ребрами — встречи, закончившиеся не вничью. По условию, в графе нет циклов длины 3 (треугольников). Покажем, что максимум числа ребер (минимум ничьих) достигается на двудольном графе. Легко видеть, что в двудольном графе может быть не менее 12 ничьих. При этом возможен случай (см. рисунок), когда ничьих ровно 12.
Если в графе есть цикл длины 5, то в этом пятиугольнике нет диагоналей (иначе образуется треугольник) — получаем уже пять ничьих. Каждый из трех оставшихся шахматистов должен свести вничью хотя бы три партии с шахматистами из этой пятерки — получаем еще не менее 3 × 3 = 9 ничьих. Еще одна ничья должна быть во встрече между этими тремя оставшимися шахматистами. Итого в этом случае будет не менее 5 + 9 + 1 = 15 ничьих, что более 12. Если есть цикл длины 7, то либо в этом семиугольнике нет диагоналей (тогда получаем уже 14 ничьих), либо диагональ, отсекающая треугольник (противоречие условию), либо диагональ, отсекающая пятиугольник - тогда сводим случай к предыдущему, получаем, что и в этом случае минимум не достигается. Граф двудольный тогда и только тогда, когда в нем нет циклов нечетной длины. Перебирая возможные двудольные графы на 8 вершинах (2-6, 4-4), получаем минимум на указанном выше графе, отсюда минимальное число ничьих 12. |
16 Апреля 2004 21:36 Раздел каталога :: Ссылка на задачу
|