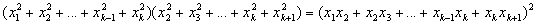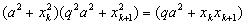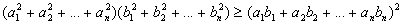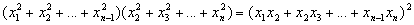358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/4 финала. Вариант 1 (8)
г.Рыбинск(2) - Школа №36(г.Ярославль) (1 февраля 2001 года)
Бесконечная последовательность чисел x1, x2, x3, …, xn, … (x1 ¹ 0) при любом n ³ 3 удовлетворяет условию
Доказать, что x1, x2, x3, …, xn, … являются последовательными членами геометрической прогрессии. |
Решение 1 (метод математической индукции). База индукции. При n = 3 равенство
приводится к виду
откуда
то есть эти числа образуют геометрическую прогрессию. Предположим, утверждение доказано для n = k (k ³ 3), q — знаменатель прогрессии. Докажем, что утверждение верно и для n = k + 1. Пусть
x2 = qx1, x3 = qx2, …, xk = qxk–1. Тогда из равенства
следует, что
откуда (xkq – xk+1)a2 = 0 или xk+1 = xkq, что и требовалось доказать. Решение 2 (неравенство Коши-Буняковского). Для любых последовательностей a1, a2, …, an и b1, b2, …, bn выполняется
причем равенство выполняется только в том случае, когда a1 / b1 = a2 / b2 = … = an / bn. Тогда для последовательностей x1, x2, …, xn–1 и x2, x3, …, xn равенство
выполняется только если x1 / x2 = x2 / x3 = … = xn–1 / xn, откуда следует, что данная прогрессия — геометрическая. |
16 Апреля 2004 21:01 Раздел каталога :: Ссылка на задачу
|
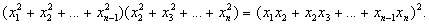
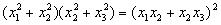
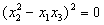
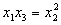
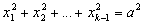 ;
;