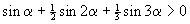1/8 финала. Вариант 2 (8)

1.

В десятичной записи некоторого натурального числа встречаются цифры 1, 3, 7, 9. Доказать, что, переставив цифры можно получить десятичную запись числа, делящегося на 7.

2.

Определенная на всей числовой оси функция f удовлетворяет при любых x и y соотношению f (x + y) = f (x) × f(y) – f (xy) + 1, причем f (1) = 2. Найдите f (m) для любого целого m.

3.

Диагонали некоторого плоского четырехугольника, последовательные стороны которого имеют длины a, b, c, d, перпендикулярны. Доказать, что диагонали любого другого плоского четырехугольника, последовательные стороны которого имеют те же длины a, b, c, d, также перпендикулярны.

4.

Существует ли такое целое число, которое при зачеркивании первой цифры уменьшается:
а) в 57 раз; б) в 58 раз?

5.

В коробке лежит 2000 спичек. Двое игроков по очереди делают ходы. За ход разрешается взять из коробка не более половины имеющихся в нем спичек. Проигрывает тот, кто не может сделать ход. Кто выиграет при правильной игре?

6.

На клетчатой плоскости дано 5 произвольных узлов целочисленной сетки (то есть точки, обе координаты каждой из которых — целые числа). Докажите, что середина одного из отрезков, соединяющих какие-то две из этих точек, также является узлом сетки.

7.

Доказать, что если стороны треугольника ABC связаны соотношением a² + b² = kc², то k > 0,5.

8.

Доказать, что для всех положительных углов a < 180° выполняется неравенство: