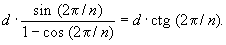358
475
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/8 финала. Вариант 1 (8)
Задачи боя "Школа №36 – Школа №86"
25 ноября 2000 года
Через точку А проведено n лучей под углами 2p / n. На одном из них на расстоянии d от А взята точка В, из нее опущен перпендикуляр на соседний луч и так далее до бесконечности. Найти длину L получаемой таким образом бесконечно завивающейся вокруг А ломаной. |
Угол между соседними лучами равен 2p / n. Обозначим через d1, d2, … расстояния от A до оснований перпендикуляров, последовательно опускаемых на лучи, исходящие из точки A. Тогда dk = d × (cos 2p/n)k. Длина k-го перпендикуляра равна Lk = dk–1 × sin 2p/n = d × sin 2p/n × (cos 2p/n)k–1. Полная длина ломаной равна: d × sin 2p/n × (1 + (cos 2p/n) + (cos 2p/n)2 + …). По формуле суммы бесконечной убывающей геометрической прогрессии длина ломаной равна
|
17 Марта 2004 21:18 Раздел каталога :: Ссылка на задачу
|