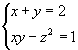1/16 финала. Вариант 5 (8)

1.

Из концов диаметра AB проведены хорды AC и BD, которые пересекаются в точке M. Докажите, что величина выражения AC × AM + BD × BM постоянна для данной окружности.

2.

Дана шахматная доска 8 ´ 8. Король стоит на поле a1. Играют двое, ходы делают по очереди. За один ход короля можно передвинуть на одно поле вправо, или на одно поле вверх, или на одно поле по диагонали "вправо-вверх". Выигрывает тот, кто поставит короля на поле h8. Кто выиграет при правильной игре?

3.

Решить в целых числах систему уравнений:

4.

Вычислительное устройство вычитает из каждого трехзначного числа сумму кубов его цифр. Какое число нужно ввести в устройство, чтобы результат оказался максимальным?

5.

После представления "Ревизора" состоялся следующий диалог:

Бобчинский: Это Вы, Петр Иванович, первый сказали "Э!". Вы сами так говорили.
Добчинский: Нет, Петр Иванович, я так не говорил. Это Вы семгу первый заказали. Вы и сказали "Э!". А у меня зуб во рту со свистом.
Бобчинский: Что я семгу первый заказал, это верно. И верно, что у Вас зуб со свистом. А все-таки, это Вы первый сказали "Э!".

Выясните, кто первым сказал "Э!", если известно, что из девяти произнесенных в этом диалоге фраз-утверждений четное число верных.

6.

Докажите, что если котангенсы углов треугольника образуют арифметическую прогрессию, то и квадраты сторон этого треугольника образуют арифметическую прогрессию.

7.

Последовательность строится по следующему закону. На первом месте стоит число 7, далее за каждым числом стоит сумма цифр его квадрата, увеличенная на 1. Какое число стоит на 2000 месте?

8.

Докажите, что в любой компании найдутся два человека, имеющие равное число знакомых в этой компании (если A знаком с B, то и B знаком с A).