358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
1/16 финала. Вариант 4 (8)
Задачи боя Школа №33 (2) – Школа №87
18 ноября 2000 года
На плоскости дано n окружностей, n ³ 5. Любые три из них пересекаются в одной точке. Доказать, что все окружности пересекаются в одной точке. |
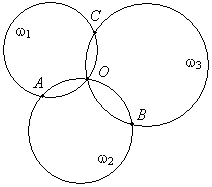
Если какие-то две окружности касаются, то все окружности проходят через точку касания. Пусть любые две окружности имеют две общие точки. Пусть окружности w1, w2, w3 пересекаются, как показано на рисунке.
Рассмотрим окружность w4. Если она не проходит через точку O, то w4 — это окружность, описанная вокруг треугольника ABC. Тогда окружность w5 должна совпадать с одной из первых четырех окружностей, чего быть не может. Значит, все окружности проходят через точку O. |
17 Марта 2004 17:53 Раздел каталога :: Ссылка на задачу
|