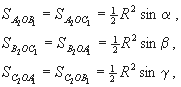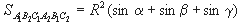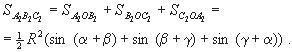358
476
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига и лига 9 классов (8)
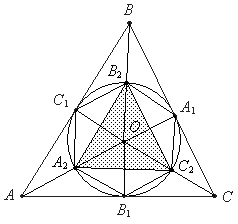
В треугольник ABC вписана окружность с центром O, которая касается сторон BC, CA, AB соответственно в точках A1, B1, C1. Отрезки AO, BO, CO пересекают окружность в точках A2, B2, C2. Докажите, что площадь треугольника A2B2C2 равна половине площади шестиугольника B1A2C1B2A1C2. |
ÐAOC1 = ÐAOB1 = a;
причем a + b + g = 180° (см. рисунок). Тогда
откуда
Найдем площадь треугольника А2В2С2:
Но из равенства a + b + g = 180° следует, что sin (a + g) = sin b,
Отсюда, с учётом полученных выражений для сравниваемых площадей, следует требуемый результат. |
Автор: В. Произволов. |
28 Февраля 2004 22:55 Раздел каталога :: Ссылка на задачу
|
 Заметим, что
Заметим, что