358
473
всего разделов:
активных пользователей:
30 мартра 2005
Форумы снова функционируют.
21 декабря 2004
Видимо в связи с обнаруженными дырами в phpBB, форум был взломан, а через него взломано и всё остальное содержимое ceemat.ru. Всё кроме форума восстановлено, ведется дискуссия по поводу его сохранения.
Приносим извинения за неудобства.
29 сентября 2004
Форум обновился до версии 2.0.10
15 мая 2004
Новый раздел: "Программирование"
16 апреля 2004 года
Задачи Ярославского турнира математических боев — 124 задачи с решениями.
29 марта 2004
Таллинская викторина: занимательные вопросы и задачи для увлеченных химией.
Высшая лига и лига 9 классов (8)
| Страницы: 1 | |
1. | Докажите, что для любых положительных чисел a, b и c выполняется неравенство: a(b + c)2 + b(c + a)2 + c(a + b)2 < (a + b + c)3 / 2. |
28 Февраля 2004 22:51 | |
2. | В ряд выписаны числа от 1 до 50 в некотором порядке. Разрешается менять местами два числа, если разность номеров их позиций равна наибольшему общему делителю этих чисел. Можно ли такими операциями получить произвольное расположение чисел? |
28 Февраля 2004 22:52 | |
3. | Натуральные числа от 1 до 22 записаны в такой последовательности a1, a2, …, a22, что
Чему равна сумма |
28 Февраля 2004 22:54 | |
4. | Натуральное число n называется приятным, если каждый выпуклый |
28 Февраля 2004 22:55 | |
5. | В треугольник ABC вписана окружность с центром O, которая касается сторон BC, CA, AB соответственно в точках A1, B1, C1. Отрезки AO, BO, CO пересекают окружность в точках A2, B2, C2. Докажите, что площадь треугольника A2B2C2 равна половине площади шестиугольника B1A2C1B2A1C2. |
28 Февраля 2004 22:55 | |
6. | По окружности расставлены в некотором порядке натуральные числа от 1 до n. Для каждой пары соседних чисел вычисляется их произведение. Какое наименьшее значение может принимать наибольшее из этих произведений? |
28 Февраля 2004 22:59 | |
7. | Два квадрата 10 ´ 10 одинаково раскрашены в 3 цвета, причем никакие две соседние (по стороне) клетки не покрашены в один цвет. Каждый квадрат разрезали произвольным образом на прямоугольники 2 ´ 1. Из частей одного квадрата составили новый квадрат 10 ´ 10. Всегда ли из частей второго квадрата можно составить квадрат, окрашенный таким же образом? |
28 Февраля 2004 23:05 | |
8. | На доску размером 11 ´ 11 клеток положили несколько квадратов размером 2 ´ 2 клетки так, что каждый квадрат закрывает 4 клетки и любые два квадрата пересекаются не более чем по одной клетке. Какое наибольшее число квадратов могли положить? |
28 Февраля 2004 23:00 | |
| Страницы: 1 | |
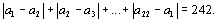 .
.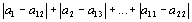 ?
?